如图，在矩形ABCD中，AB=3，BC=5，BE平分∠ABC交AD于点E．连接CE，点F是BE上一动点，过点F作FG∥CE交BC于点G．将△BFG绕点B旋转得到△BF'G'．
（1）连接CG'，EF'，求证：△BEF'∽△BCG'；
（2）当点G'恰好落在直线AE上时，若BF=3，求EG'的值．
【答案】（1）证明过程详见解答；
（2）EG′=．
（2）EG′=
6
±
14
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/25 6:0:3组卷：504引用：2难度：0.5
相似题
-
1．如图，点D是△ABC中AB边上一点，以AD为直径的⊙O与BC相切于点C，连接CD．
（1）判断△BCD与△BAC是否相似？并说明理由．
（2）若⊙O的半径为3，tan∠BCD=，求BC的长度．12发布：2025/5/23 14:30:1组卷：175引用：1难度：0.5 -
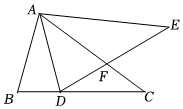2．如图，在△ABC中，AB＜AC，将△ABC以点A为中心逆时针旋转得到△ADE，点D在BC边上，DE交AC于点F．下列结论：①△AFE∽△DFC；②DA平分∠BDE；③∠CDF=∠BAD，其中正确结论的个数是（ ）发布：2025/5/23 15:0:2组卷：199引用：1难度：0.6 -
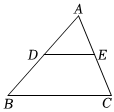3．如图，DE是△ABC的中位线，S△ADE=1，则S△ABC=．发布：2025/5/23 15:0:2组卷：185引用：3难度：0.5
