在矩形ABCD中，BC=2AB，E是BC中点，连接AE，DE，点F是射线BE上一动点（不与点B，E重合），过点F作FG⊥AF交直线DE于点G．
（1）如图1，若点F是BE中点，猜想AF与FG的数量关系：AF ==FG．
（2）若F是线段BE上任意一点，其他条件不变（1）中的猜想还成立吗？若成立，请给予证明，若不成立请说明理由．
（3）若点F是射线BE上一点，EF=2，AB=6，则FG=213或10213或10（请直接写出FG的长）．
13
13
【考点】四边形综合题．
【答案】=；2或10
13
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/10 8:0:8组卷：35引用：1难度：0.3
相似题
-
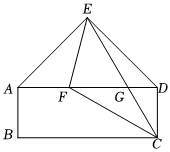1．在五边形ABCDE中，四边形ABCD是矩形，△ADE是以E为直角顶点的等腰直角三角形．CE与AD交于点G，将直线EC绕点E顺时针旋转45°交AD于点F．
（1）求证：∠AEF=∠DCE；
（2）判断线段AB，AF，FC之间的数量关系，并说明理由；
（3）若FG=CG，且AB=2，求线段BC的长．发布：2025/5/24 8:0:1组卷：328引用：2难度：0.2 -
2．[问题提出]
正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系？
[问题探究]
如图①，△ABC是等边三角形，半径OA=R，∠AOB是中心角，P是△ABC内任意一点，P到△ABC各边距离PF、PE、PD分别为h1、h2、h3，设△ABC的边长是a,面积为S．过点O作OM⊥AB．
∴OM=Rcos∠AOB=Rcos60°，AM=Rsin12∠AOB=Rsin60°，AB=2AM=2Rsin60°12
∴S△ABC=3S△AOB=3×AB×OM=3R2sin60°cos60°①12
∵S△ABC又可以表示为a（h1+h2+h3）②12
联立①②得a（h1+h2+h3）=3R2sin60°cos60°12
∴×2Rsin60°（h1+h2+h3）=3R2sin60°cos60°12
∴h1+h2+h3=3Rcos60°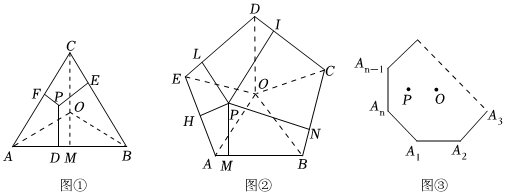
[问题解决]
如图②，五边形ABCDE是正五边形，半径OA=R，∠AOB是中心角，P是△ABC内任意一点，P到△ABC各边距PH、PM、PN、PI、PL分别为h1、h2、h3、h4、h5，参照（1）的分析过程，探究h1+h2+h3+h4+h5的值与正五边形ABCDE的半径R及中心角的关系．
[性质应用]
（1）正六边形（半径是R）内任意一点P到各边距离之和h1+h2+h3+h4+h5+h6=．
（2）如图③，正n边形（半径是R）内任意一点P到各边距离之和h1+h2+hn-1+hn=．发布：2025/5/24 8:0:1组卷：149引用：1难度：0.2 -
3．四边形ABCD为正方形，AB=8，点E为直线BC上一点，射线AE交对角线BD于点F，交直线CD于点G．
（1）如图，点E在BC延长线上．求证：△CFG∽△EFC；
（2）是否存在点E，使得△CFG是等腰三角形？若存在，求BE的长；若不存在，请说明理由．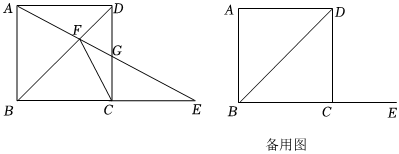
发布：2025/5/24 7:0:1组卷：57引用：1难度：0.1
