综合与实践
根据以下素材，探索完成任务．
| 如何设计纸盒 | ||
| 素材1 | 利用一边长为40cm的正方形纸板可设计成如图1和图2所示的两种纸盒，图1是无盖的纸盒，图2是一个有盖的纸盒． |
|
| 素材2 | 如图，若在正方形硬纸板的四角各剪掉一个同样大小的小正方形，将剩余部分折成一个无盖的长方体盒子． |
|
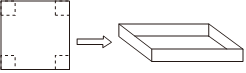
| 问题解决 | ||
| 任务1 | 初步探究：折一个底面积为484cm2的无盖长方体盒子． | 问剪掉的小正方形的边长为多少？ |
| 任务2 | 探究折成的无盖长方体盒子的侧面积能否为800cm2？ | 如果能，求出此时剪掉的小正方形的边长；如果不能，说明理由． |
| 任务3 | 图3是一个高为4cm的无盖的五棱柱盒子（直棱柱），图4是其底面，在五边形ABCDE中，AE=DE，BC=12cm,AB=DC=6cm,∠ABC=∠BCD=120°，∠EAB=∠EDC=90°． |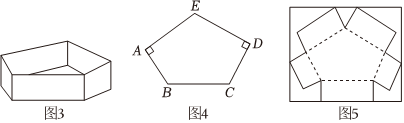
图3中的五棱柱盒子可按图5所示的示意图，将矩形纸板剪切折合而成，那么这个矩形纸板的长和宽至少各为多少厘米？请直接写出结果．（图中实线表示剪切线，虚线表示折痕，纸板厚度及剪切接缝处损耗忽略不计） |
【考点】几何变换综合题．
【答案】任务1：剪掉的小正方形的边长为9cm；
任务2：剪掉的小正方形的边长为10cm；
任务3：矩形纸板的长至少为18+4，矩形纸板的宽至少为4+8．
任务2：剪掉的小正方形的边长为10cm；
任务3：矩形纸板的长至少为18+4
3
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/11 18:0:9组卷：265引用：3难度：0.1
相似题
-
1．将线段AB绕点A逆时针旋转60°得到线段AC，继续旋转α（0°＜α＜120°）得到线段AD，连接CD．
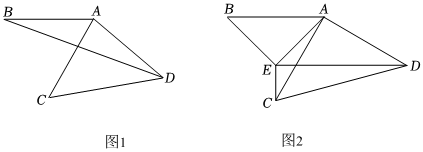
（1）连接BD，
①如图1，若α=80°，则∠BDC的度数为 ；
②在第二次旋转过程中，请探究∠BDC的大小是否改变．若不变，求出∠BDC的度数；若改变，请说明理由．
（2）如图2，以AB为斜边作直角三角形ABE，使得∠B=∠ACD，连接CE，DE．若∠CED=90°，求α的值．发布：2025/6/23 16:0:1组卷：633引用：8难度：0.1 -
2．如图，△ABC为边长是4
的等边三角形，四边形DEFG是边长是6的正方形．现将等边△ABC和正方形DEFG按如图①的方式摆放，使点C与点E重合，点B、C、E、F在同一条直线上，△ABC从图①的位置出发，以每秒1个单位长度的速度沿EF方向向右匀速运动，当点B与点E重合时停止运动，设△ABC的运动时间为t秒．3
（1）当点A与点D重合时，求此时t的值；
（2）在整个运动过程中，设等边△ABC和正方形DEFG重叠部分的面积为S，求S与t之间的函数关系式；
（3）如图②，当点A与点D重合时，作∠ABE的角平分线BM交AE于点M，将△ABM绕点A逆时针旋转，使边AB与边AC重合，得到△ACN．在线段AG上是否存在H点，使得△ANH为等腰三角形？若存在，求线段AH的长度；若不存在，请说明理由．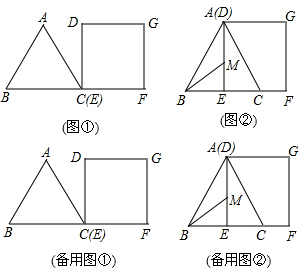
发布：2025/6/24 11:30:1组卷：111引用：1难度：0.3 -
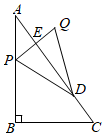3．如图，在△ABC中，∠ABC=90°，AB=4，BC=3，点P从点A出发，沿折线AB-BC以每秒5个单位长度的速度向点C运动，同时点D从点C出发，沿CA以每秒2个单位长度的速度向点A运动，点P到达点C时，点P、D同时停止运动，当点P不与点A、C重合时，作点P关于直线AC的对称点Q，连结PQ交AC于点E，连结DP、DQ，设点P的运动时间为t秒．
（1）当点D与点E重合时，求t的值．
（2）用含t的代数式表示线段CE的长．
（3）当△PDQ为直角三角形时，求△PDQ与△ABC重叠部分的面积．发布：2025/6/25 5:0:1组卷：45引用：1难度：0.1
