在平面直角坐标系中，点O为坐标原点，直线AB的解析式为y=kx+6（k≠0），交x轴的负半轴于点A，交y轴的正半轴于点B，且OA=OB．
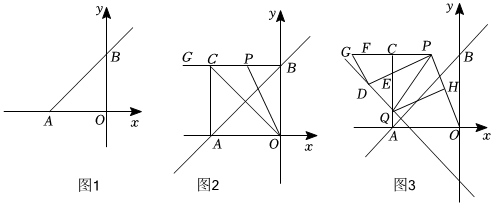
（1）如图1，求k的值；
（2）如图2，AC∥y轴，BG∥x轴交AC于点C，点P为BC上一点，连接OP、OC，设点P的横坐标为t,△COP的面积为S，求S与t的函数关系式；（不要求写出自变量t的取值范围）；
（3）如图3，在（2）的条件下，作PD⊥PO，PD=PO，∠AOP的平分线OF交DP于点E、交BG于点F，连接DG，且DG∥PO，FG：DE=1：4，点H为PO的中点，点Q为AC上一点，连接PQ、OQ、HQ、DQ，若∠PQH+∠POQ=90°，求直线DQ的解析式．
【考点】一次函数综合题．
【答案】（1）k=1．
（2）S=3t+18．
（3）y=-x-．
（2）S=3t+18．
（3）y=-
119
120
1183
240
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/2 8:0:8组卷：85引用：1难度：0.2
相似题
-
1．如图，在平面直角坐标系中，B（-8，0），∠B=45°．
（1）如图1，求直线AB的解析式；
（2）如图2，点P、Q在直线AB上，点P在第二象限，横坐标为t,点Q在第一象限，横坐标为d,PQ=AB，求d与t之间的函数关系式（不要求写出自变量的取值范围）；
（3）如图3，在（2）的条件下，点C、点D在x轴的正半轴上（C在D的左侧），连接AC、AD，∠ADO=2∠CAO，OC=2CD，点E是AC中点，连接DE、QE、QD，若S△DEQ=24，求t值．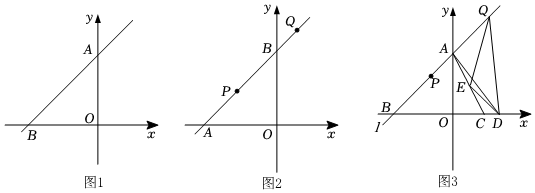
发布：2025/5/26 4:30:1组卷：213引用：1难度：0.1 -
2．【阅读材料】
我们知道：一条直线经过等腰直角三角形的直角顶点，过另外两个顶点分别向该直线作垂线，即可得“三垂直模型”．如图①，在△ABC中，∠ACB=90°，AC=BC，分别过A、B向经过点C的直线作垂线，垂足分别为D、E，易证：△ADC≌△CEB．（无需证明）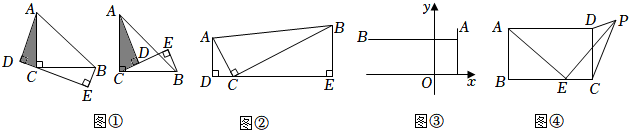
（1）【问题探究】如果AC≠BC，其他条件不变，如图②，求证：△ADC∽△CEB．
（2）【学以致用】如图③，在平面直角坐标系中，∠AOB=90°，点A（1，2），点B在第二象限，，求AB所在直线的函数表达式．tanA=32
（3）【拓展应用】如图④，在矩形ABCD中，AB=4，BC=6，点E为边BC上一个动点，连结AE，将线段AE绕点E顺时针旋转90°，点A落在点P处，当点P在矩形ABCD外部时，连结PC、PD．当△DPC为直角三角形时，直接写出BE的长．发布：2025/5/26 11:0:2组卷：269引用：1难度：0.2 -
3．如图，直线y=
x+6分别与x轴、y轴交于点A、B，点C为线段AB上一动点（不与A、B重合），以C为顶点作∠OCD=∠OAB，射线CD交线段OB于点D，将射线OC绕点O顺时针旋转90°交射线CD于点E，连结BE．34
（1）证明：=CDDB；（用图1）ODDE
（2）当△BDE为直角三角形时，求DE的长度；（用图2）
（3）点A关于射线OC的对称点为F，求BF的最小值．（用图3）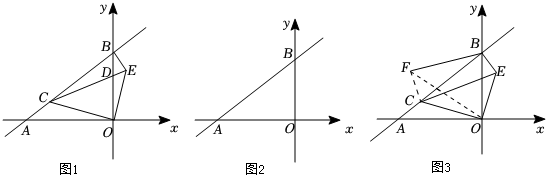
发布：2025/5/26 7:30:2组卷：1837引用：4难度：0.2
