（1）根据下列叙述填依据：
已知：如图①，AB∥CD，∠B+∠BFE=180°，求∠B+∠BFD+∠D的度数．
解：因为∠B+∠BFE=180°
所以AB∥EF（同旁内角互补，两直线平行同旁内角互补，两直线平行 ）
因为AB∥CD（已知已知 ）
所以CD∥EF（如果两条直线都与第三条直线平行，那么这两条直线也平行如果两条直线都与第三条直线平行，那么这两条直线也平行 ）
所以∠CDF+∠DFE=180°（两直线平行，同旁内角互补两直线平行，同旁内角互补 ）
所以∠B+∠BFD+∠D=∠B+∠BFE+∠EFD+∠D=360°
（2）根据以上解答进行探索，如图②，AB∥EF，∠BDF与∠B、∠F有何数量关系
（3）你能探索处图③、图④两个图形中，∠BDF与∠B、∠F的数量关系吗？请写出来．
【考点】平行线的判定与性质．
【答案】同旁内角互补，两直线平行；已知；如果两条直线都与第三条直线平行，那么这两条直线也平行；两直线平行，同旁内角互补
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：545引用：2难度：0.3
相似题
-
1．如图，AB∥CD∥FH∥GM，且∠EFH=∠GMN．
（1）求证：EG∥HN；
（2）若∠AEG=75°，求∠HNC．发布：2025/6/13 17:0:1组卷：159引用：1难度：0.7 -
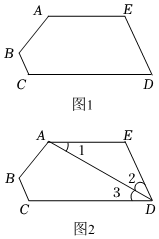2．如图1，在五边形ABCDE中，AE∥CD，∠E=∠C．
（1）猜想BC与DE之间的位置关系，并说明理由；
（2）如图2，连接AD，若AD平分∠CDE，∠C=4∠1-18°，求∠C的度数．发布：2025/6/14 19:30:1组卷：19引用：1难度：0.7 -
3．完成下列推理过程：如图，已知∠A=∠EDF，∠C=∠F，求证：BC∥EF．
证明：∵∠A=∠EDF（已知），
∴∥（ ），
∴∠C=（ ）．
又∵∠C=∠F（已知），
∴=∠F（等量代换），
∴∥（ ）．发布：2025/6/13 18:30:2组卷：234引用：3难度：0.6
