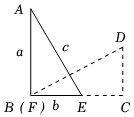
将两个全等的直角三角形按如图所示的方式放置，三角形的长直角边记为a,短直角边记为b,斜边记为c,试通过各部分图形面积之间的数量关系验证勾股定理．

【答案】见解析．

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/8/11 20:0:1组卷：56引用：2难度：0.7

相似题

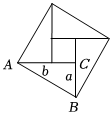1．如图，“赵爽弦图”由4个全等的直角三角形所围成，在Rt△ABC中，AC=b,BC=a,∠ACB=90°，若图中大正方形的面积为35，小正方形的面积为3，则（a+b）²的值为
．
发布：2025/5/24 13:0:1组卷：69引用：1难度：0.6
解析
2．小慧在课外阅读时遇到了一个与勾股定理有关的故事：古希腊哲学家柏拉图对勾股定理很有研究，曾得到勾股数的一个结论：如果m表示大于1的整数，则a=2m,b=m²-1，c=m²+1构成勾股数，你能证明柏拉图这个结论吗？并利用这个结论写出两组勾股数．（勾股数定义：若三角形三边长a、b、c都是正整数，且满足a²+b²=c²，那么a、b、c称为一组勾股数）．
发布：2025/5/25 1:0:1组卷：28引用：1难度：0.5
解析
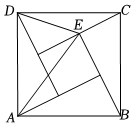3．汉代数学家赵爽为了证明勾股定理，构造了一副“弦图”，后人称其为“赵爽弦图”．如图，大正方形ABCD由四个全等的直角三角形和一个小正方形组成，若∠ADE=∠AED，
AD
=
2
5
，则△ADE的面积为（　　）
A．6 B．5 C．
2
5
D．
2
10
发布：2025/5/25 11:30:2组卷：357引用：3难度：0.5
解析

1．如图，“赵爽弦图”由4个全等的直角三角形所围成，在Rt△ABC中，AC=b,BC=a,∠ACB=90°，若图中大正方形的面积为35，小正方形的面积为3，则（a+b）2的值为 ．