如图1，直线MN与直线AB、CD分别交于点E、F，∠1与∠2互补．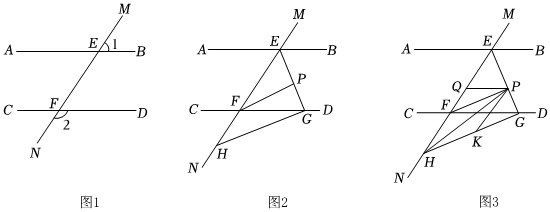
（1）试判断直线AB与直线CD的位置关系，并说明理由；
（2）如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH；
（3）如图3，在（2）的条件下，连接PH，K是GH上一点使∠PHK=∠HPK，作PQ平分∠EPK，问∠HPQ的大小是否发生变化？若不变，请直接写出其值．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/28 8:0:9组卷：406引用：7难度：0.5
相似题
-
1．如图，已知CD⊥AB，EF⊥AB，垂足分别为D，F，∠B+∠BDG=180°，试说明∠BEF=∠CDG．将下面的解答过程补充完整，并填空（填写理由依据或数学式）．
证明：∵CD⊥AB，EF⊥AB（已知），
∴∠BFE=∠BDC=90°（），
∴EF∥CD（），
∴∠BEF=（），
又∵∠B+∠BDG=180°（），
∴BC∥DG，
∴∠CDG=（），
∴∠CDG=∠BEF（）．发布：2025/6/9 5:30:2组卷：416引用：4难度：0.4 -
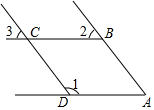2．如图，一个由4条射线构成的图案，其中∠1=125°，∠2=55°，∠3=55°
（1）写出图中相互平行的射线，并证明；
（2）直接写出∠A的度数（不需要证明）发布：2025/6/9 3:30:1组卷：26引用：2难度：0.7 -
3．完成下面的填空．
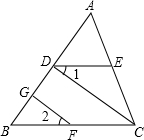
如图，已知FG⊥AB，CD⊥AB，垂足分别为G，D，∠1=∠2．
证明：∠CED+∠ACB=180°
请你将小明的证明过程补充完整．
证明：∵FG⊥AB，CD⊥AB，垂足分别为G，D（已知），
∴∠FGB=∠CDB=90° （ ）．
∴GF∥CD（ ）．
∵GF∥CD（已证），
∴∠2=∠BCD （ ）．
又∵∠1=∠2（已知），
∴∠1=∠BCD （ ）．
∴DE∥BC （ ）．
∴∠CED+∠ACB=180° （ ）．发布：2025/6/9 2:30:1组卷：221引用：3难度：0.7
