课外兴趣小组活动时，老师提出了如下问题：
如图①，△ABC中，若AB=12，AC=6，求BC边上的中线AD的取值范围．
小明在组内经过合作交流，得到了如下的解决方法：延长AD至点E，使DE=AD，连接BE．由此可证△ADC≌△EDB，从而得到BE=AC=6，再根据△ABE三边关系得出AD取值范围．
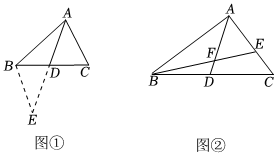
（1）小明解题过程中证出△ADC≌△EDB的依据是 AA；
A．SAS
B．SSS
C．AAS
D．HL
请参考小明的解题思路回答以下问题：
（2）如图②，AD是△ABC的中线，BE交AC于E，交AD于F，且AE=EF．若EF=4，EC=3，求线段BF的长．
【答案】A
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/14 8:0:9组卷：681引用：3难度：0.4
相似题
-
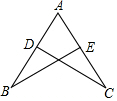1．已知AB=AC，BD=CE，求证：∠B=∠C．发布：2025/6/8 9:0:1组卷：1010引用：12难度：0.8 -
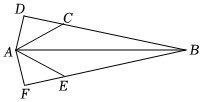2．如图，已知AD，AF分别是钝角△ABC和钝角△ABE的高，如果AD=AF，AC=AE．
（1）求证：BC=BE；
（2）若∠DBF=∠BAC=30°，AC=4，求AD的长．发布：2025/6/8 7:30:1组卷：76引用：1难度：0.5 -
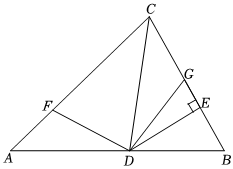3．如图，在△ABC中，CD是△ABC的角平分线，DE⊥BC于E，F，G分别是边AC，BC上的点，连接DF，DG，若DF=DG，△CDF和△DEG的面积分别为50和15，则△CDG的面积为 ．发布：2025/6/8 7:30:1组卷：436引用：5难度：0.5
