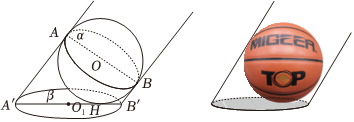
小明同学某天发现，在阳光下的照射下，篮球在地面留下的影子如图所示，设过篮球的中心O且与太阳平行光线垂直的平面为α，地面所在平面为β，篮球与地面的切点为H，球心为O，球心O在地面的影子为点O'；已知太阳光线与地面的夹角为θ；
（1）求平面α与平面β所成角φ（用θ表示）；
（2）如图，AB为球O的一条直径，A′、B'为A、B在地面的影子，点H在线段A′B'上，小明经过研究资料发现，当θ≠π2时，篮球的影子为一椭圆，且点H为椭圆的焦点，线段A′B'为椭圆的长轴，求此时该椭圆的离心率（用θ表示）．
θ
≠
π
2
【考点】椭圆的几何特征；二面角的平面角及求法．
【答案】（1）；
（2）e=cosθ．
π
2
-
θ
（2）e=cosθ．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/25 4:0:2组卷：49引用：1难度：0.5
相似题
-
1．已知椭圆
=1（a＞b＞0）的一个焦点为F（2，0），椭圆上一点P到两个焦点的距离之和为6，则该椭圆的方程为（ ）x2a2+y2b2发布：2024/12/29 12:30:1组卷：12引用：2难度：0.7 -
2．已知椭圆C的两焦点分别为
、F1（-22，0），长轴长为6．F2（22，0）
（1）求椭圆C的标准方程；
（2）求以椭圆的焦点为顶点，以椭圆的顶点为焦点的双曲线的方程．发布：2024/12/29 11:30:2组卷：442引用：6难度：0.8 -
3．阿基米德（公元前287年-公元前212年）不仅是著名的物理学家，也是著名的数学家，他利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积．若椭圆C的对称轴为坐标轴，焦点在x轴上，且椭圆C的离心率为
，面积为8π，则椭圆C的方程为（ ）32发布：2024/12/29 12:0:2组卷：229引用：7难度：0.5
