【阅读新知】19世纪英国著名文学家和历史学家卡莱尔给出了一元二次方程x2+bx+c=0的几何解法：如图1，在平面直角坐标系中，已知点A（0，1）、B（-b,c），以AB为直径作⊙P．若⊙P交x轴于点M（m,0）、N（n,0），则m、n为方程x2+bx+c=0的两个实数根．
【探究新知】
（1）由勾股定理得，AM2=12+m2，BM2=c2+（-b-m）2，AB2=（1-c）2+b2．
在Rt△ABM中，AM2+BM2=AB2，所以12+m2+c2+（-b-m）2=（1-c）2+b2．
化简得：m2+bm+c=0．同理可得：n2+bn+c=0n2+bn+c=0．
所以m、n为方程x2+bx+c=0的两个实数根．
【运用新知】
（2）在图2中的x轴上画出以方程x2-4x-2=0两根为横坐标的点M、N．
（3）已知点A（0，1）、B（-10，25），以AB为直径作⊙C．判断⊙C与x轴的位置关系，并说明理由．
【拓展提升】
（4）在平面直角坐标系中，已知两点A（0，a）、B（-b,c），若以AB为直径的圆与交x轴有两个交点M、N，则以点M、N的横坐标为根的一元二次方程是 x2+bx+ac=0x2+bx+ac=0．
【考点】圆的综合题．
【答案】n2+bn+c=0；x2+bx+ac=0
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/4 7:0:9组卷：184引用：1难度：0.1
相似题
-
1．如图，⊙O的半径为5，弦BC=6，A为BC所对优弧上一动点，△ABC的外角平分线AP交⊙O于点P，直线AP与直线BC交于点E．
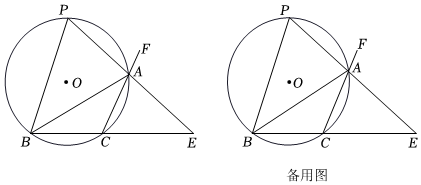
（1）求证：P为优弧BAC的中点；
（2）连接PC，求PC的长度；
（3）求sin∠BAC的值；
（4）若△ABC为非锐角三角形，请直接写出△ABC的面积的最大值．发布：2025/6/15 3:0:1组卷：97引用：1难度：0.1 -
2．【数学概念】
有一条对角线平分一组对角的四边形叫“对分四边形”．
【概念理解】
（1）关于“对分四边形”，下列说法正确的是 ．（填所有正确的序号）
①菱形是“对分四边形”
②“对分四边形”至少有两组邻边相等
③“对分四边形”的对角线互相平分
【问题解决】
（2）如图①，PA为⊙O的切线，A为切点．在⊙O上是否存在点B、C，使以P、A、B、C为顶点的四边形是“对分四边形”？
请根据小明的作法补全图形，并证明四边形PACB是“对分四边形”．小明的作法：
①以P为圆心，PA长为半径作弧，与⊙O交于点B；
②连接PO并延长，交⊙O于点C；
③点B、C即为所求．
（3）如图②，已知线段AB和直线l,请在图②中利用无刻度的直尺和圆规，在直线l上作出点M、N，使以A、B、M、N为顶点的四边形是“对分四边形”．（只要作出一个即可，不写作法，保留作图痕迹）
（4）如图③，⊙O的半径为5，AB是⊙O的弦，AB=8，点C是⊙O上的动点，若存在四边形ABCD是“对分四边形”，且有一条边所在的直线是⊙O的切线，直接写出AC的长度．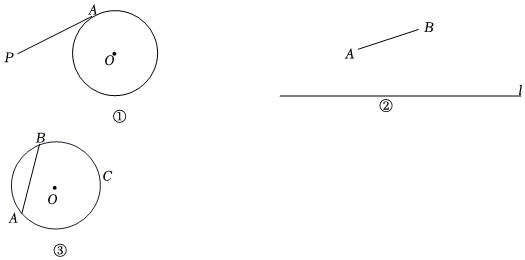
发布：2025/6/14 20:30:2组卷：977引用：3难度：0.1 -
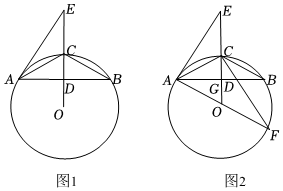3．如图，⊙O为△ABC的外接圆，AC=BC，D为OC与AB的交点，E为线段OC延长线上一点，且∠EAC=∠ABC．
（1）求证：直线AE是⊙O的切线．
（2）若CD=6，AB=16，求⊙O的半径；
（3）在（2）的基础上，点F在⊙O上，且=ˆBC，△ACF的内心点G在AB边上，求BG的长．ˆBF发布：2025/6/14 23:0:1组卷：1104引用：7难度：0.1
