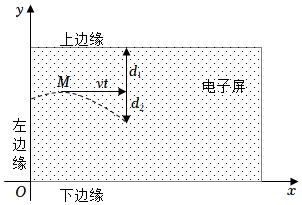
某电子屏上下边缘距离为9cm,点P在电子屏上的运动路线如图中虚线所示，当运动至点M时达到最高点，此时距左边缘2cm,之后的运动时间为t秒，点P是下落过程中某位置：水平方向继续以速度vcm/s向右运动，竖直方向与电子屏上边缘距离为dcm,d由两部分组成：d1为常数，d2与t的平方成正比，且有如表格中的数据．
| t | d |
| t=1 | d=3.2 |
| t=2 | d=3.8 |
（2）若v=2，用t（t＞2）分别表示点P的横坐标x、纵坐标y,求y与x之间的关系式，并求点P在电子屏左边缘时的坐标；
（3）甲、乙两点从左边缘不同位置出发，均能达到最高点M，若乙点比甲先出发ms,v甲=2，v乙=1，在两点下落过程中，若某时刻甲恰好处于乙正上方，且距离不小于1.2cm,直接写出m的最小值．
【考点】二次函数的应用．
【答案】（1）d=0.2t2+3，M（2，6）；
（2）y=-（x-2）2+6，（0，5.8）；
（3）．
（2）y=-
1
20
（3）
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：344引用：3难度：0.5
相似题
-
1．某公司电商平台在之前举行的商品打折促销活动中不断积累经验，经调查发现，某种进价为a元的商品周销售量y（件）关于售价x（元/件）的函数关系式是y=-3x+300（40≤x≤100），如表仅列出了该商品的售价x,周销售量y,周销售利润W（元）的一组对应值数据．【周销售利润=（售价-进价）×周销售量】
（1）求该商品进价a；x y W 40 180 3600
（2）该平台在获得的周销售利润额W（元）取得最大值时，决定售出的该商品每件捐出m元给当地福利院，若要保证捐款后的利润率不低于20%，求m的最大值．发布：2025/5/24 18:30:1组卷：78引用：1难度：0.6 -
2．已知某商品的进价为每件10元，我班数学兴趣小组经过市场调查，整理出该商品在第x（1≤x≤30）天的售价与销量的相关信息如下表：
（1）第几天该商品的销售单价是25元？第x天 1≤x＜15 15≤x≤30 日销售单价（元/千克） 20+ x1210+ 300x日销售量（千克） 40-x
（2）在这30天中，第几天获得的利润最大？最大利润是多少？发布：2025/5/24 18:0:1组卷：172引用：2难度：0.6 -
3．九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如表：
已知该商品的进价为每件30元，设销售该商品的每天利润为y元．时间x（天） 1≤x＜50 50≤x≤90 售价（元/件） x+40 90 每天销量（件） 200-2x
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？发布：2025/5/24 18:30:1组卷：341引用：3难度：0.3
