如图1，已知等边三角形ABC的边长为3，点M，N分别是边AB，AC上的点，且BM=2MA，AN=2NC．
如图2，将△AMN沿MN折起到△A'MN的位置，连接A'B，A'C．
（1）求证：平面A'BM⊥平面BCNM；
（2）给出三个条件：①A'M⊥BC；②二面角A'-MN-C的大小为60°；③A'到平面BCNM的距离为22．从中任选一个，补充在下面问题的条件中，并作答：
已知_______，在线段A'C上是否存在一点P，使三棱锥A'-PMB的体积为34？若存在，求出A′PA′C的值；若不存在，请说明理由．
2
2
3
4
A
′
P
A
′
C
【考点】平面与平面垂直；二面角的平面角及求法．
【答案】（1）证明见解答；（2）选①存在P，满足条件，且；选②存在P，满足条件，且；选③不存在P，满足条件．
A
′
P
A
′
C
=
3
2
A
′
P
A
′
C
=
1
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/6 8:0:9组卷：103引用：2难度：0.4
相似题
-
1．如图，AB是圆O的直径，C是圆周上一点，PA⊥平面ABC．
（1）求证：平面PAC⊥平面PBC；
（2）若D也是圆周上一点，且与C分居直径AB的两侧，试写出图中所有互相垂直的各对平面．发布：2025/1/20 8:0:1组卷：20引用：1难度：0.5 -
2．如图△ABC内接于圆O，G，H分别是AE，BC的中点，AB是圆O的直径，四边形DCBE为平行四边形，且DC⊥平面ABC．证明：
（1）GH∥平面ACD；
（2）平面ACD⊥平面ADE．发布：2025/1/20 8:0:1组卷：9引用：1难度：0.3 -
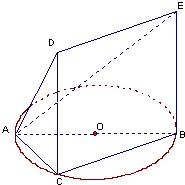3．如图，△ABC内接于圆O，AB是圆O的直径，AB=2，BC=1，DC=，四边形DCBE为平行四边形，DC⊥平面ABC．3
（1）求三棱锥C-ABE的体积；
（2）证明：平面ACD⊥平面ADE；
（3）在CD上是否存在一点M，使得MO∥平面AE？证明你的结论．发布：2025/1/20 8:0:1组卷：25引用：1难度：0.5
