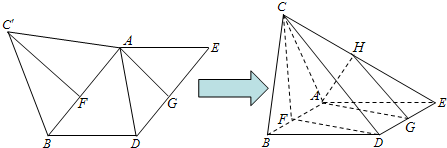
如图，一个正△ABC'和一个平行四边形ABDE在同一个平面内，其中AB=8，BD=AD=43，AB，DE的中点分别为F，G．现沿直线AB将△ABC'翻折成△ABC，使二面角C-AB-D为120°，设CE中点为H．
（Ⅰ）（i）求证：平面CDF∥平面AGH；（ii）求异面直线AB与CE所成角的正切值；
（Ⅱ）求二面角C-DE-F的余弦值．
43
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：11引用：1难度：0.5
相似题
-
1．教室内墙面与地面所成的二面角度数为
.发布：2024/12/12 10:0:2组卷：28引用：1难度：0.8 -
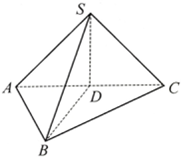2．在三棱锥S-ABC中，已知△ABC是边长为4的正三角形，平面SAC⊥平面ABC，D为AC的中点，且.求：SA=SC=22
（1）二面角A-SD-B的大小；
（2）三棱锥S-ABC的体积.发布：2025/1/2 18:30:1组卷：43引用：1难度：0.7 -
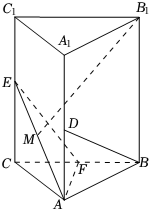3．如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥平面ABC，△ABC为正三角形，且，E、F分别为CC1，BC的中点．AB=2AA1=22
（1）求证：EF⊥平面AB1F；
（2）求锐二面角B1-AE-F的大小．发布：2025/1/2 19:30:2组卷：30引用：1难度：0.3
