阅读下列材料并完成任务：
数学活动课上，老师让同学们探究用尺规作图作一条直线的平行线．如图1，已知在∠AOB中，点M、N分别在射线OA、OB上，且OM=ON，点P在线段OB上，求作直线PQ，使PQ∥MN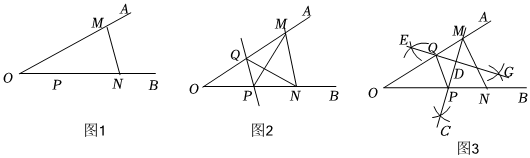． 小琦的作图方法：如图2，连接MP，作∠QNP=∠PMQ，NQ 交OA于点Q，作直线PQ，则PQ∥MN． （1）①通过师生讨论，小琦的解法得到赞同，下面是小琦不完整的证明过程请补充完成． ∵∠PMO=∠QNP，OM=ON，∠O=∠O，∴△PMO≌△QNO，∴ OP=OQ OP=OQ ，∴∠OPQ=∠OQP ∠OPQ=∠OQP ，∴∠OPQ=1 2 1 2 ∠OPQ=∠ONM ∠OPQ=∠ONM ，∴PQ∥MN PQ∥MN .小颖：我认为小琦的作图方法很有创意，但是太麻烦了，可以改进如下，如图3，作∠OMN 的角平分线MC交OB于点P，作MP的垂直平分线EG交OM于点Q，连接PQ，则PQ∥MN．… |
任务：②小琦得出△PMO≌△QNO，的依据是
④
④
（填序号）．①SSS
②SAS
③AAS
④ASA
（2）小颖的作法正确吗？若正确，请加以证明；
（3）如图4，已知∠AOB=30°，点M、N分别在射线OA、OB上，且OM=ON，点P是射线OB上的一动点，点Q是射线OA上的一动点，当∠PMQ=∠QNP=45°时，请直接写出
S
△
OPQ
S
△
PQM
【考点】三角形综合题．
【答案】OP=OQ；∠OPQ=∠OQP；∠OPQ=∠ONM；PQ∥MN；④
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/12 8:0:9组卷：112引用：1难度：0.1
相似题
-
1．（1）如图1，在△ABC中，∠ACB=2∠B，CD平分∠ACB，交AB于点D，DE∥AC，交BC于点E．
①若DE=1，BD=，求BC的长；32
②试探究-ABAD是否为定值．如果是，请求出这个定值；如果不是，请说明理由．BEDE
（2）如图2，∠CBG和∠BCF是△ABC的2个外角，∠BCF=2∠CBG，CD平分∠BCF，交AB的延长线于点D，DE∥AC，交CB的延长线于点E．记△ACD的面积为S1，△CDE的面积为S2，△BDE的面积为S3．若S1•S3=916，求cos∠CBD的值．S22
发布：2025/6/10 12:30:1组卷：4095引用：8难度：0.3 -
2．已知△ABC是边长为4的等边三角形，点D是射线BC上的动点，将AD绕点A逆时针方向旋转60°得到AE，连接DE．
（1）如图1，猜想△ADE是什么三角形？；（直接写出结果）
（2）如图2，点D在射线CB上（点C的右边）移动时，证明∠BCE+∠BAC=180°．
（3）点D在运动过程中，△DEC的周长是否存在最小值？若存在．请求出△DEC周长的最小值；若不存在，请说明理由．发布：2025/6/10 12:30:1组卷：278引用：2难度：0.1 -
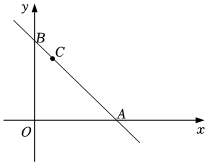3．如图，在平面直角坐标系中，点A（4，0），B（0，4）．点C为线段AB上一点．
（1）∠OBA=；
（2）若BC=，点P的横坐标为3，求OP+CP的最小值；2
（3）连接OC，使∠BOC=15°，点M是直线AB上一动点，以OM为边在OM的下方作等边△OMN，连接CN，求CN的最小值．发布：2025/6/10 15:0:1组卷：304引用：2难度：0.1
