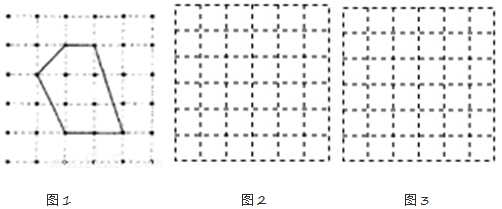
各顶点都在方格纸格点（横竖格子线的交错点）上的多边形称为格点多边形．如何计算它的面积？奥地利数学家皮克（G•Pick,1859～1942年）证明了格点多边形的面积公式S=a+12b-1，其中a表示多边形内部的格点数，b表示多边形边界上的格点数，S表示多边形的面积．如图，a=4，b=6，S=4+12×6-1=6
（1）请在图1中画一个格点正方形，使它的内部只含有4个格点，并写出它的面积．
（2）请在图2中画一个格点三角形，使它的面积为72，且每条边上除顶点外无其它格点．
1
2
1
2
7
2
【考点】作图—应用与设计作图．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：773引用：30难度：0.5
相似题
-
1．如图是由36个边长为1的小正方形拼成的网格图，请按照下列要求作图．
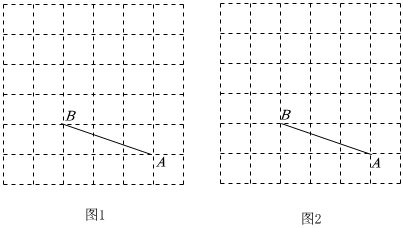
（1）在图1中画出一个以AB为边的Rt△ABC；
（2）在图2中画出一个以AB为底边的等腰△ABC．发布：2025/6/7 1:0:2组卷：66引用：2难度：0.5 -
2．图1、图2分别是10×6的网格，网格中每个小正方形的边长均为1，各个小正方形的顶点叫做格点，A、B两点在格点上，请在下面的网格中按要求分别画图，使得每个图形的顶点均在格点上．
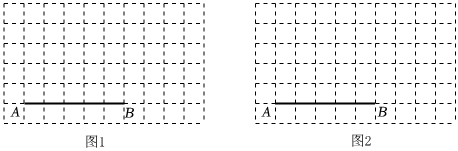
（1）在图1中画一个△ABC，使△ABC为钝角等腰三角形，且△ABC的面积为10；
（2）在图2中画一个平行四边形ABEF，使其周长为10+213
（3）在图2中连接BF，并直接写出BF的长，BF=．发布：2025/6/7 3:0:1组卷：23引用：2难度：0.5 -
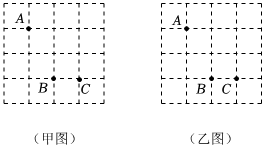3．如图，在4×4的正方形网格中，每一个小正方形的边长均为1，网格中有三个点A，B，C，要求作一个四边形使这三个点在这个四边形内或上（包括边或顶点），且四边形的顶点在网格的顶点上．
（1）在甲图中画出一个面积为4的平行四边形；
（2）在乙图中画出一个面积最小的菱形．发布：2025/6/7 3:30:1组卷：16引用：2难度：0.7
