数形结合是解决数学问题的一种重要的思想方法，借助这种方法可将抽象的数学知识变得直观，从而可以帮助我们快速解题，初中数学里的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释．
（1）如图①，在Rt△ABC中，∠ACB=90°，BC=a,AC=b,AB=c,以Rt△ABC的三边长向外作正方形的面积分别为S1，S2，S3，请直接写出S1，S2，S3之间存在的等量关系为 S1+S2=S3S1+S2=S3；
（2）如图②，如果以Rt△ABC的三边长a,b,c为直径向外作半圆，那么（1）中的结论是否成立？请说明理由；
（3）如图③，在Rt△ABC中，∠ACB=90°，三边长分别为5，12，13，分别以它的三边长为直径向上作半圆，求图③中阴影部分的面积．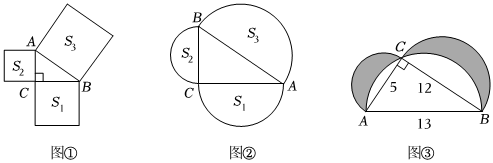
【答案】S1+S2=S3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/15 13:0:8组卷：295引用：5难度：0.5
相似题
-
1．在△ABC中，BC=a,AC=b,AB=c,若∠C=90°，如图1，则有a2+b2=c2；若△ABC为锐角三角形，小明猜想：a2+b2＞c2．理由如下：
如图2，过点A作AD⊥CB于点D，设CD=x.
在Rt△ADC中，AD2=b2-x2；
在Rt△ADB中，AD2=c2-（a-x）2．
∴b2-x2=c2-（a-x）2，即a2+b2=c2+2ax.
∵a＞0，x＞0，
∴2ax＞0，
∴a2+b2＞c2．
故当△ABC为锐角三角形时，a2+b2＞c2．
∴小明的猜想是正确的．
请你猜想，当△ABC为钝角三角形时，如图3，a2+b2与c2的大小关系，并证明你猜想的结论．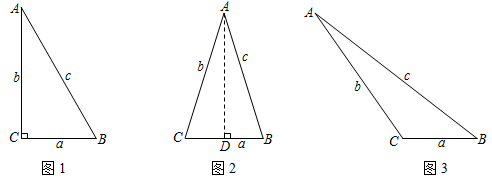
发布：2025/6/17 8:30:1组卷：156引用：1难度：0.5 -
2．如图，在四边形ABCD中，AD∥BC，AB=3，BC=5，连接BD，∠BAD的平分线分别交BD、BC于点E、F，且AE∥CD
（1）求AD的长；
（2）若∠C=30°，求CD的长．发布：2025/6/17 7:30:2组卷：252引用：8难度：0.3 -
3．（1）已知两点A（-3，m），B（2m,4），且A和B到x轴距离相等，求B点坐标．
（2）点A在第四象限，当m为何值时，点A（m+2，3m-5）到x轴的距离是它到y轴距离的一半．发布：2025/6/17 8:0:1组卷：44引用：1难度：0.8
