我们知道，函数y=f（x）的图象关于原点成中心对称图形的充要条件是函数y=f（x）为奇函数，有同学发现可以将其推广为：函数y=f（x）的图象关于点P（a,b）成中心对称图形的充要条件是函数y=f（x+a）-b为奇函数（1）设函数f（x）=x3-3x2+1
（ⅰ）求函数f（x）图象的对称中心，并求f（-2019）+f（-2020）+f（-2021）+f（2021）+f（2022）+f（2023）的值；
（ⅱ）若函数y=f（x）与函数g（x）=1x-1-1图象有两个交点A，B，若点C坐标为（0，2），求|CA+CB|的值．
（2）类比上述推广结论，写出“函数y=f（x）的图象关于y轴成轴对称图形的充要条件是函数y=f（x）为偶函数”的一个推广结论．
g
（
x
）
=
1
x
-
1
-
1
|
CA
+
CB
|
【考点】类比推理．
【答案】（1）（i）=-6；（ii）2；
（2）函数y=f（x）的图象关于直线x=a成轴对称图形的充要条件是函数y=f（x+a）为偶函数．
10
（2）函数y=f（x）的图象关于直线x=a成轴对称图形的充要条件是函数y=f（x+a）为偶函数．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/16 8:0:9组卷：45引用：2难度：0.6
相似题
-
1．已知
tan（x+π4）=1+tanx1-tanx，那么函数y=tanx的周期为π．类比可推出：已知x∈R且（x≠kπ+π4），那么函数y=f（x）的周期是（ ）f（x+π）=1+f（x）1-f（x）发布：2025/1/6 8:0:1组卷：11引用：1难度：0.7 -
2．阅读下表后，请应用类比的思想，得出椭圆中的结论：
圆 椭圆 定
义平面上到动点P到定点O的距离等于定长的点的轨迹 平面上的动点P到两定点F1，F2的距离之和等于定值2a的点的轨迹（2a＞|F1F2|） 结
论如图，AB是圆O的直径，直线AC，BD是圆O过A，B的切线，P是圆O上任意一点，
CD是过P的切线，则有“PO2=PC•PD”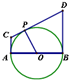
椭圆的长轴为AB，O是椭圆的中心，F1，F2是椭圆的焦点，直线AC，BD是椭圆过A，B的切线，P是椭圆上任意一点，CD是过P的切线，则有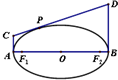 
发布：2025/1/28 8:0:2组卷：32引用：2难度：0.5 -
3．若
，x≠kπ+π4，则y=tanx的周期为π．类比可推出：设x∈R且tan（x+π4）=1+tanx1-tanx，则y=f（x）的周期是（ ）f（x+π）=1+f（x）1-f（x）发布：2025/1/6 8:0:1组卷：36引用：1难度：0.5
