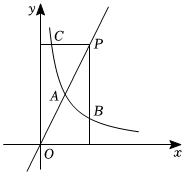
在平面直角坐标系xOy中，函数y=kx（x＞0）的图象与一次函数y=2x的图象交于点A（a,2）．
（1）求a,k的值；
（2）点P是射线OA上一点，过点P分别作x轴，y轴的垂线交函数y=kx（x＞0）的图象于点B，C．将线段PB，PC和函数y=kx（x＞0）的图象在点B，C之间的部分所围成的区域（不含边界）记为W，我们把横、纵坐标都是整数的点叫做整点．利用函数图象解决下列问题：
①若点P的横坐标是2，则区域W内整点的坐标为 （1，3）（1，3）；S△PAB=3232；
②若区域W内恰有5个整点，则点P的横坐标xP的取值范围为 2＜xP≤522＜xP≤52．
y
=
k
x
（
x
＞
0
）
y
=
k
x
（
x
＞
0
）
y
=
k
x
（
x
＞
0
）
3
2
3
2
2
＜
x
P
≤
5
2
2
＜
x
P
≤
5
2
【考点】反比例函数与一次函数的交点问题．
【答案】（1，3）；；
3
2
2
＜
x
P
≤
5
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/18 8:0:9组卷：597引用：2难度：0.5
相似题
-
1．如图，一次函数y=kx+b与反比例函数y=的图象相交于A（2，3），B（-3，n）两点．mx
（1）求一次函数与反比例函数的解析式；
（2）根据所给条件，请直接写出不等式kx+b＞的解集；mx
（3）过点B作BC⊥x轴，垂足为C，求S△ABC．发布：2025/5/27 18:30:2组卷：2431引用：47难度：0.5 -
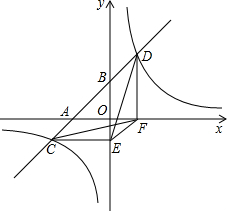2．如图，一次函数y=ax+b的图象与x轴、y轴交于A、B两点，与反比例函数的图象相交于C、D两点，分别过C、D两点作y轴，x轴的垂线，垂足为E、F，连接CF、DE，有下列结论：①△CEF与△DEF的面积相等；②EF∥CD；③△DCE≌△CDF；④AC=BD；⑤△CEF的面积等于y=kx，其中正确的个数是（ ）k2发布：2025/5/27 20:0:1组卷：1140引用：10难度：0.9 -
3．如图，已知直线与双曲线y=12x交于A、B两点，且点A的横坐标为4．y=kx（k＞0）
（1）求k的值；
（2）若双曲线上一点C的纵坐标为8，求△AOC的面积；y=kx（k＞0）
（3）根据图象回答：当x取何值时，反比例函数的值大于一次函数的值．发布：2025/5/27 12:30:2组卷：140引用：1难度：0.3
