请阅读以下材料，并完成相应的任务．
| 【阅读材料】 在《阿基米德全集》中的《引理集》中记述了伟大的古希腊数学家、哲学家、物理学家阿基米德提出的六个有关圆的引理，其中第二个引理是： 如图1，点P是 ˆ AB ˆ AB ˆ PQ ˆ PA  |
（1）如图2，小明同学尝试说明“BQ=BD”，于是他连接了PA，PB，PD，PQ，请根据小明的思路完成后续证明过程；
（2）如图3，以AB为直径的半圆上有一点P，AP=6，AB=10，直线l与⊙O相切于点P，过点B作BE⊥l于点E，交⊙O于点Q，求出BQ的长．
【考点】圆的综合题．
【答案】（1）见解析；
（2）．
（2）
14
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/25 18:0:8组卷：289引用：6难度：0.5
相似题
-
1．问题提出：
（1）如图①，已知线段AB，试在其上方确定一点C，使∠ACB=90°，且△ABC的面积最大，请画出符合条件的△ABC．
问题探究：
（2）如图②，在矩形ABCD中，点E在BC边上，且BE=3CE，连接DE、AE，若AE=12，求△AED面积的最大值．
问题解决：
（3）某市新建成一迎宾广场，园林部门准备在“三•八”节前，用少量资金对广场一角进行绿化美化改造，以提升城市形象．根据地形特点，准备设计一个由三条线段AD、AB、BC及一段组成的区域，并在其内部栽花种草进行美化．如图③所示，ˆCD在以AB为直径的半圆上，圆心为O，AB=12米，为保证最佳观赏效果，要求ˆCD的长为2π，已知栽花种草每平方米费用为50元（含所有花费），园林部门准备了2600元用于上述区域的绿化工作，请问是否可满足本次绿化美化改造最大费用的需求？（参考数据ˆCD≈1.73，π≈3.14）3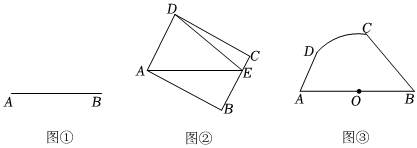
发布：2025/5/24 13:0:1组卷：540引用：1难度：0.1 -
2．已知在Rt△ABC中，∠C=90°，AC=
，BC=2．23
（1）如图①，若P为BC上由点B向点C运动的一点，连接AP，设AP的中点为G，求在点P运动的过程中，点G经过的路径长．
（2）如图②，若P是以AB为直径所作半圆上由点A沿着半圆向点B运动的一点，求CP的中点F经过的路径长．
（3）如图③，若P为BC上由点B向点C运动的一点，连接AP，作BR⊥AP于点R，（P、R可以重合）求在点P的运动过程中，R经过的路径长．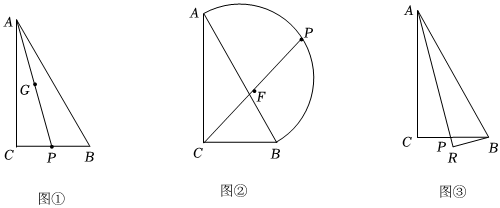
发布：2025/5/24 13:30:2组卷：86引用：1难度：0.3 -
3．如图1，在Rt△ABC中，∠ABC=90°，以线段BC为直径作⊙O交AC于点D，E为AB中点，连接ED，过点C作CF∥AB交ED的延长线于点F．
（1）求证：直线ED是⊙O的切线；
（2）判断△CDF的形状，并说明理由；
（3）如图2，连接OF交⊙O于点P，连接BP交AC于点Q，若D为AQ中点，AB=6，求PQ的长．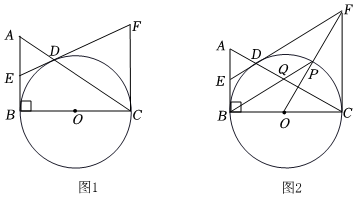
发布：2025/5/24 13:30:2组卷：319引用：2难度：0.3
