在正方体ABCD-A1B1C1D1中，已知AB=1，Q是棱DD1上的动点（可与D、D1重合）．
（1）当Q是DD1中点时，画出过A，Q，B1的截面；
（2）是否存在点Q在棱DD1上，且满足BQ⊥面AB1C，并说明理由；
（3）设DQ=x,过A，Q，B1三点的截面面积为S（x），求函数y=S（x）的表达式并求出值域．
【考点】直线与平面垂直；平面的基本性质及推论．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/14 16:0:50组卷：79引用：1难度：0.5
相似题
-
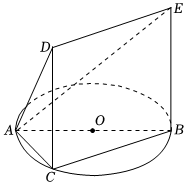1．≜如图，一简单组合体的一个面ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，且DC⊥平面ABC．
（1）证明：BC⊥平面ACD；
（2）若AB=2，BC=1，tan∠EAB=，试求该简单组合体的体积V．32发布：2025/1/20 8:0:1组卷：25引用：1难度：0.5 -
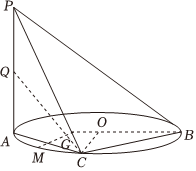2．如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆O上异于A，B的点，
（1）求证：BC⊥平面PAC；
（2）设Q，M分别为PA，AC的中点，问：对于线段OM上的任一点G，是否都有QG∥平面PBC？并说明理由．发布：2025/1/28 8:0:2组卷：35引用：2难度：0.3 -
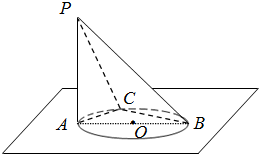3．如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆周上不同于A、B的任意一点．
（1）求证：BC⊥平面PAC；
（2）求证：平面PAC⊥平面PBC．发布：2025/1/28 8:0:2组卷：124引用：3难度：0.3
