如图，取一副三角板按图1拼接，固定三角板ADE（∠AED=30°的Rt△），将三角板ABC（∠ACB=45°的Rt△）绕点A顺时针旋转一个大小为α的角（0°＜c≤45°），试问：
（1）当α=1515度时，能使图2中的AB∥DE；
（2）当α=4545度时，能使图3中的AB与AE重合；
（3）当0°＜a≤45°时，连接BD（如图4），探求∠DBC+∠CAE+∠BDE的值的大小变化情况，并说明理由．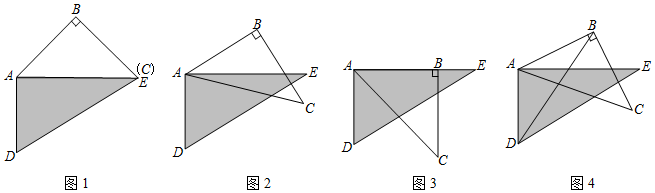
【考点】平行线的判定与性质．
【答案】15；45
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/22 8:0:9组卷：382引用：2难度：0.4
相似题
-
1．在横线处填写依据：
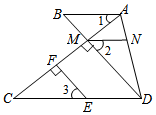
如图所示．已知：EF⊥AC．垂足为点F，DM⊥AC，垂足为点M，DM的延长线交AB于点B，且∠1=∠C，点N在AD上，且∠2=∠3，试说明AB∥MN．
解∵EF⊥AC，DM⊥AC，
∴∠CFE=∠CMD=90° （ ）
∴EF∥DM （ ）
∴∠3=∠CDM （ ）
∵∠3=∠2（已知），
∴∠2=∠CDM（等量代换），
∴MN∥CD （ ）
∴∠AMN=∠C （ ）
∵∠1=∠C（已知），
∠1=∠AMN（等量代换），
∴AB∥MN （ ）．发布：2025/6/8 18:30:1组卷：164引用：4难度：0.7 -
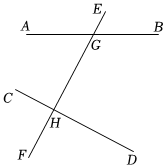2．如图，直线AB，CD被直线EF所截，交点分别为G，H，∠CHG=∠DHG=∠AGE．34
（1）CD与EF有怎样的位置关系？请说明理由．
（2）求∠CHG的同位角、内错角、同旁内角的度数．发布：2025/6/8 18:30:1组卷：31引用：2难度：0.5 -
3．完成下面的推理填空：
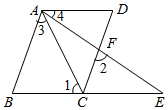
如图，已知AB∥CD，∠1=∠2，∠3=∠4，求证：∠D=∠DCE．
证明：∵AB∥CD，
∴∠2=∠BAE（ ）．
∵∠BAE=∠3+，
∴∠2=∠3+，
∵∠3=∠4，
∴∠2=∠CAD，
又∵∠2=，
∴∠CAD=，
∴AD∥（ ）．
∴∠D=∠DCE（ ）．发布：2025/6/8 18:30:1组卷：1259引用：8难度：0.6
