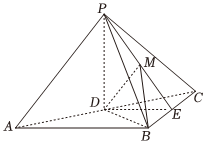
如图，三棱锥P-ABC的底面为等腰直角三角形，∠ABC=90°，AB=2．D，E分别为AC，BC的中点，PD⊥平面ABC，点M在线段PE上．
（1）从下面的①、②、③、④四个条件中选择两个作为已知，使得平面MBD⊥平面PBC，并给予证明；
条件①：PD=2；条件②：PD=3；条件③：PM=3ME；条件④：PE=3ME．
（2）在（1）的条件下，求直线BP与平面MBD所成的角的正弦值．
2
3
【答案】（一）当选择①④时：
（1）证明过程见解答．
（2）．
（二）当选择②③时：
（1）证明过程见解答；
（2）．
（1）证明过程见解答．
（2）
1
2
（二）当选择②③时：
（1）证明过程见解答；
（2）
3
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/3 11:0:1组卷：37引用：1难度：0.4
相似题
-
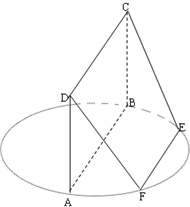1．AB为圆O的直径，点E，F在圆上，AB∥EF，矩形ABCD所
在平面与圆O所在平面互相垂直，
已知AB=2，EF=1．
（1）求证：BF⊥平面DAF；
（2）求BF与平面ABCD所成的角；
（3）若AC与BD相交于点M，
求证：ME∥平面DAF．发布：2025/1/20 8:0:1组卷：29引用：3难度：0.1 -
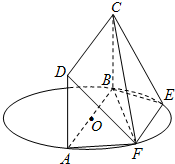2．如图，AB为圆O的直径，点E，F在圆上，AB∥EF，矩形ABCD所在平面与圆O所在平面互相垂直，已知AB=2，EF=1．
（Ⅰ）求证：BF⊥平面ADF；
（Ⅱ）求BF与平面ABCD所成的角；
（Ⅲ）在DB上是否存在一点M，使ME∥平面ADF？若不存在，请说明理由；若存在，请找出这一点，并证明之．发布：2025/1/20 8:0:1组卷：23引用：3难度：0.3 -
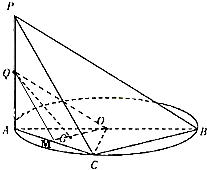3．如图，AB是圆O的直径，PA垂直圆O所在的平面，C是圆O上的点．
（1）求证：BC⊥平面PAC；
（2）设Q为PA的中点，G△AOC的重心，求证：QG∥平面PBC．
（3）若AC=BC=，PC与平面ACB所成的角为3，求三棱锥P-ACB的π3
体积．发布：2025/1/20 8:0:1组卷：74引用：1难度：0.7
