知识生成：我们已经知道，通过计算几何图形的面积可以表示一些代数恒等式．例如：由图①可以得到（a+b）2=a2+2ab+b2，基于此，请解答下列问题：
直接应用：（1）若xy=5，x+y=7，直接写出x2+y2的值为 3939；
类比应用：（2）填空：①若x（4-x）=2，则x2+（x-4）2= 1212；
②若（x-3）（x-5）=2，则（x-3）2+（x-5）2= 88；
知识迁移：（3）如图②，一农家乐准备在原有长方形用地（即长方形ABCD）上进行装修和扩建，先用长为120m的装饰性篱笆围起该长方形用地，再以AD，CD为边分别向外扩建正方形ADGH、正方形DCEF的空地，并在这两块正方形空地上建造功能性花园，该功能性花园面积和为2000m2，求原有长方形用地ABCD的面积．
【考点】完全平方公式的几何背景；单项式乘多项式．
【答案】39；12；8
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/1 8:0:9组卷：155引用：3难度：0.7
相似题
-
1．如图，有一个边长为a的大正方形和两个边长为b的小正方形，分别将它们按照图①和图②的形式摆放．
（1）用含有a、b的代数式分别表示阴影面积：S1=S2=，S3=．
（2）若a+b=10，ab=24，求2S1-3S3的值；
（3）若S1=12，S2=10，S3=18，求出图③中的阴影部分面积．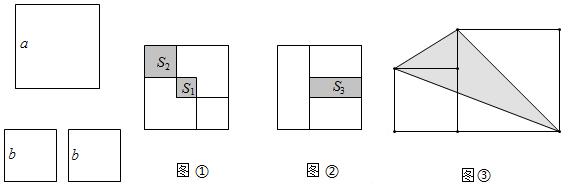
发布：2025/6/20 5:0:1组卷：890引用：4难度：0.5 -
2．有3张边长为a的正方形纸片，4张边长分别为a、b（b＞a）的矩形纸片，5张边长为b的正方形纸片，从其中取出若干张纸片，每种纸片至少取一张，把取出的这些纸片拼成一个正方形（按原纸张进行无空隙、无重叠拼接），则拼成的正方形的边长最长可以为（ ）
发布：2025/6/19 11:30:1组卷：3332引用：74难度：0.9
