（1）问题发现
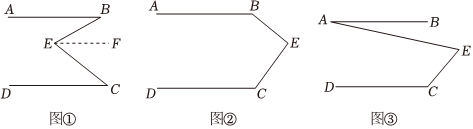
如图①，直线AB∥CD，E是AB与AD之间的一点，连接BE，CE，可以发现∠B+∠C=∠BEC．请把下面的证明过程补充完整．
证明：过点E作EF∥AB．
（2）拓展探究
如果点E运动到图②所示的位置，其他条件不变，求证：∠B+∠C=360°-∠BEC．
（3）解决问题
如图③，AB∥DC，∠C=120°，∠AEC=80°，求∠A度数．
【考点】平行线的判定与性质．
【答案】（1）见解析；
（2）见解析；
（3）20°．
（2）见解析；
（3）20°．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/6 8:0:9组卷：73引用：2难度：0.5
相似题
-
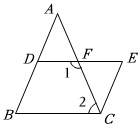
1．如图，在△ABC中，点D，E在AB边上，点F在AC边上，EF∥DC，点H在BC边上，且∠1+∠2=180°．求证：∠A=∠BDH．
请将下面的证明过程补充完整：
证明：∵EF∥DC，
∴∠2+∠=180°．（理由：）
∵∠1+∠2=180°，
∴∠1=∠．
∴∥．（理由：）
∴∠A=∠BDH．发布：2025/6/10 3:30:1组卷：394引用：4难度：0.5 -
2．如图，已知∠1+∠2=180°，∠B=∠E．
（1）试猜想AB与CE之间有怎样的位置关系？并说明理由．
（2）若CA平分∠BCE，∠B=50°，求∠A的度数．发布：2025/6/10 3:0:1组卷：2377引用：17难度：0.5 -
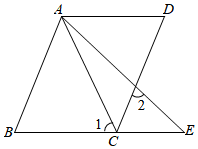3．如图，已知AB∥CD，∠B=∠D，AE交BC的延长线于点E．
（1）求证：AD∥BE；
（2）若∠1=∠2=60°，∠BAC=2∠EAC，求∠B的度数．发布：2025/6/10 4:30:1组卷：2798引用：12难度：0.7
