材料阅读：如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．
小明给出了下面一种证明的思路：
证明：在边AB上截取AE=MC，连接ME．
∵正方形ABCD中，∠B=∠BCD=90°，AB=BC，
∴∠NMC=180°-∠AMN-∠AMB，
=180°-∠B-∠AMB，
=∠MAB，
=∠MAE．
…
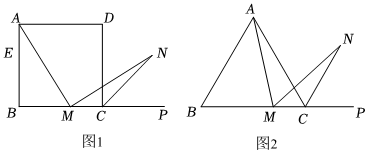
（1）若将材料阅读中的“正方形ABCD”改为“正三角形ABC”（如图2），N是∠ACP的平分线上一点，则∠AMN=60°时，结论AM=MN是否还成立？请说明理由；
（2）若将材料阅读中的“正方形ABCD”改为“正n边形ABCD...X“，请你作出猜想：当∠AMN=（n-2）•180°n（n-2）•180°n时，结论AM=MN仍然成立．（直接写出答案，不需要证明）
（
n
-
2
）
•
180
°
n
（
n
-
2
）
•
180
°
n
【答案】
（
n
-
2
）
•
180
°
n
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/18 4:0:2组卷：51引用：1难度：0.1
相似题
-
1．小明学习菱形时，对矩形ABCD进行了画图探究（AD＞AB），其作法和图形如下：
①连接BD；
②分别以点B，D为圆心，大于BD长的一半为半径作弧，两弧相交于M，N两点，作直线MN交BD于点O，交AD于点E，交BC于点F；
③连接BE，DF．
（1）根据以上作法，判断四边形BFDE的形状，并说明理由；
（2）若AB=4，AD=8，求四边形BFDE的面积．发布：2025/6/9 23:0:1组卷：109引用：5难度：0.5 -
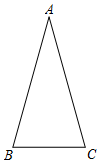2．如图，在△ABC中，AB=AC．
（1）利用尺规作图作边BC的高AD，垂足为D（保留作图痕迹，不写作法）；
（2）求证：BD=CD．
（3）如果三角形的周长是22，一边长为5，求它的另外两边长．发布：2025/6/9 22:0:2组卷：40引用：2难度：0.4 -
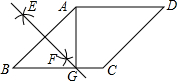3．如图，在菱形ABCD中，按以下步骤作图：
①分别以点A和B为圆心，以大于AB的长为半径作弧，两弧相交于点E、F；12
②作直线EF交BC于点G，连接AG；
若AG⊥BC，CG=3，则AD的长为．发布：2025/6/9 22:30:2组卷：321引用：3难度：0.5
