如图，已知在△ABC中，AB=BC=AC，∠BAC=∠ABC=∠ACB=60°，点P、Q分别是△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．
（1）求证：△ABQ≌△CAP；
（2）当点P、Q分别在AB、BC边上运动时，∠QMC的大小变化吗？若变化，请说明理由；若不变，求出它的度数．
（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，请直接写出它的度数．
【考点】三角形综合题．
【答案】（1）证明见解析部分；
（2）60°；
（3）120°．
（2）60°；
（3）120°．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/19 7:0:1组卷：244引用：2难度：0.2
相似题
-
1．如图1，△ACB和△ECD都是等腰直角三角形，CA=CB，CE=CD．
（1）[教材呈现]△ACB的顶点A在△ECD的斜边DE上，线段AE、AD、AC之间的数量关系为 ．
（2）[变换探究]如图2，△ACB的顶点A在△ECD的斜边DE的延长线上，且CA=CB=3，CE=CD=22，求线段AE的长．2
（3）[拓展应用]如图3，△ACB的顶点A在△ECD的斜边DE上运动（不与D、E重合），若CE=CD=2，问△ABD的面积是否有最大值？如果有，请求出这个最大值，如果没有，请说明理由．2
发布：2025/6/9 1:0:1组卷：65引用：1难度：0.3 -
2．如图，点O是等边△ABC内一点，∠AOB=110°，连接OC，将△OBC顺时针方向旋转60°得到△DAC，连接OD．
（1）求证：△COD是等边三角形；
（2）若∠BOC=150°，试判断△AOD的形状，并说明理由；
（3）试探究：当∠BOC的度数为多少时，△AOD是等腰三角形．发布：2025/6/9 1:30:1组卷：42引用：2难度：0.3 -
3．问题情境
七下教材第149页提出这样一个问题：如图1，∠AOB=90°，OC平分∠AOB，把三角尺的直角顶点落在OC的任意一点P上，并使三角尺的两条直角边分别与OA、OB相交于点E、F，PE与PF相等吗？
（1）七年级学习这部分内容时，我们还无法对这个问题的结论加以证明，八上教材第59页第11题不仅对这一问题给出了答案：“通过实验可以得到PE=PF”，还要求“现在请你证明这个结论”，请你给出证明；
变式拓展：
（2）如图2，已知∠AOB=120°，OC平分∠AOB，P是OC上一点，∠EPF=60°，PE边与OA边相交于点E，PF边与射线OB的反向延长线相交于点F．试解决下列问题：
①PE与PF还相等吗？为什么？
②试判断OE、OF、OP三条线段之间的数量关系，并说明理由．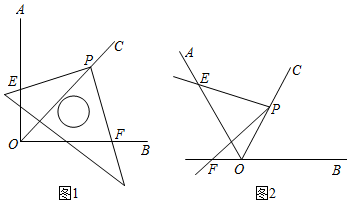
发布：2025/6/9 1:30:1组卷：471引用：3难度：0.2
