问题探究：

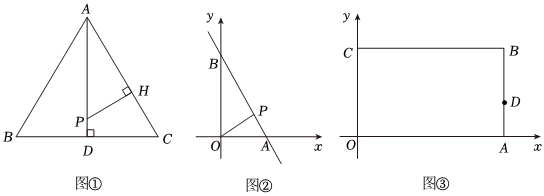
（1）如图①，在等边△ABC中，点P为高AD上的动点，过点P作PH⊥AC，垂足为点H，则

PH

AP

的值为

1

2

1

2

；
（2）如图②，在平面直角坐标系中，直线

y

=

-

3

x

+

6

与x轴、y轴分别交于点A、点B．若点P为线段AB上的动点，求

1

2

BP

+

OP

的最小值；
问题解决：
（3）如图③，在平面直角坐标系中，长方形OABC的OA边在x轴上，OC边在y轴上，且B（14，8）．点D在AB边上，且AD=3．点E在BC边上，将△DBE沿DE翻折，使得点B恰好落在OA边上的点B′处．那么在折痕DE上是否存在点P，使得

1

2

EP

+

B

′

P

最小，若存在，求出

1

2

EP

+

B

′

P

的最小值；若不存在，请说明理由．