数形结合是解决数学问题的一种重要的思想方法，借助图的直观性，可以帮助理解数学问题．
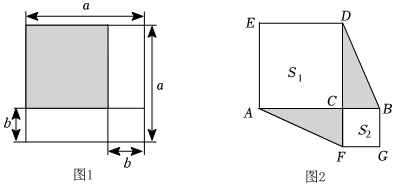
（1）如图1，阴影部分是一个边长为a的大正方形剪去一个边长为b的小正方形和两个宽为b的长方形之后所剩余的部分．用两种方式表示阴影部分的面积为 （a-b）2（a-b）2或 a2+b2-2aba2+b2-2ab，由此可以验证的公式为 （a-b）2=a2+b2+2ab（a-b）2=a2+b2+2ab；
（2）请设计一个新的图形验证公式：（a+b）2=a2+2ab+b2；
（3）如图2，S1，S2分别表示边长为a,b的正方形的面积，且A，B，C三点在一条直线上，若S1+S2=40，AB=8，求图中阴影部分的面积．
【考点】完全平方公式的几何背景；多项式乘多项式．
【答案】（a-b）2；a2+b2-2ab；（a-b）2=a2+b2+2ab
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/1 8:0:9组卷：116引用：1难度：0.7
相似题
-
1．如图，有一个边长为a的大正方形和两个边长为b的小正方形，分别将它们按照图①和图②的形式摆放．
（1）用含有a、b的代数式分别表示阴影面积：S1=S2=，S3=．
（2）若a+b=10，ab=24，求2S1-3S3的值；
（3）若S1=12，S2=10，S3=18，求出图③中的阴影部分面积．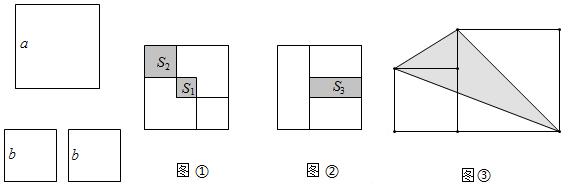
发布：2025/6/20 5:0:1组卷：890引用：4难度：0.5 -
2．有3张边长为a的正方形纸片，4张边长分别为a、b（b＞a）的矩形纸片，5张边长为b的正方形纸片，从其中取出若干张纸片，每种纸片至少取一张，把取出的这些纸片拼成一个正方形（按原纸张进行无空隙、无重叠拼接），则拼成的正方形的边长最长可以为（ ）
发布：2025/6/19 11:30:1组卷：3332引用：74难度：0.9
