已知各项都为正数的数列{an}满足a1=a（a＞2），e-an+1+an+1=-1an+kan（n∈N*），给出下列三个结论：
（1）若k=1，则数列{an}仅有有限项；
（2）若k=2，则数列{an}单调递增；
（3）若k=2，则对任意的M＞0，都存在n0∈N*，使得n02an0＞M成立．
则上述结论中正确的为（ ）
e
-
a
n
+
1
1
a
n
n
0
2
a
n
0
【考点】命题的真假判断与应用．
【答案】A
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：79引用：2难度：0.2
相似题
-
1．下面四个命题中，其中正确命题的序号为．
①函数f（x）=|tanx|是周期为π的偶函数；
②若α、β是第一象限的角，且α＞β，则sinα＞sinβ；
③是函数x=π8的一条对称轴方程；y=sin（2x+54π）
④在内方程tanx=sinx有3个解．（-π2，π2）发布：2025/1/6 8:0:1组卷：5引用：3难度：0.7 -
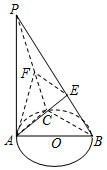2．如图，PA⊥圆O所在的平面，AB是圆O的直径，C是圆O上的一点，E、F分别是PB、PC上的点，AE⊥PB，AF⊥PC，给出下列结论：
①AF⊥PB；
②EF⊥PB；
③AF⊥BC；
④AE⊥平面PBC．
其中正确结论的序号是 ．发布：2025/1/20 8:0:1组卷：65引用：6难度：0.5 -
3．给出下列命题：
①小于90°的角是第一象限角；
②将y=sin2x的图象上所有点向右平移个单位长度可得到y=sin（2x-π3）的图象；π3
③若α、β是第一象限角，且α＞β，则sinα＞sinβ；
④函数f（x）=3sin（2x-）关于直线x=π3对称11π12
⑤函数y=|tanx|的周期和对称轴方程分别为π，x=（k∈Z）kπ2
其中正确的命题的序号是．（注：把你认为正确的命题的序号都填上）发布：2025/1/6 8:0:1组卷：3引用：2难度：0.5
相关试卷
