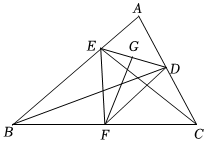
如图，在△ABC中，BD、CE分别是边AC、AB上的高线．
（1）如果BD=CE，那么△ABC是等腰三角形，请说明理由；
（2）取F为BC中点，连接点D，E，F得到△DEF，G是ED的中点，求证：FG⊥DE；
（3）在（2）的条件下，如果∠A=60°．BC=16，求FG的长度．
【考点】三角形综合题．
【答案】（1）见解析；
（2）见解析；
（3）4．
（2）见解析；
（3）4
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：275引用：3难度：0.3
相似题
-
1．如图在平面直角坐标系中，已知A（0，a），B（b,0），且a2+b2-4a-8b+20=0．
（1）求A，B两点的坐标．
（2）如图①，P是∠BOA的平分线一点，PA⊥PB于P，求P点坐标．
（3）如图②，在（2）的条件下，过P作PC⊥PO交x轴于C，求点C的坐标．发布：2025/5/29 12:30:1组卷：132引用：4难度：0.1 -
2．数学课上，刘老师出示了如下框中的题目：
小聪与同桌小明讨论后，仍不得其解．刘老师提示道：“数学中常通过把一个问题特殊化来找到解题思路”．两人茅塞顿开，于是进行了如下解答，请你根据他们提供的思路完成下面相应内容：如图，在等边△ABC中，E为线段AB上一点，D为线段CB延长线上一点，且ED=EC，试确定AE与DB的大小关系，并说明理由．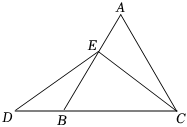 
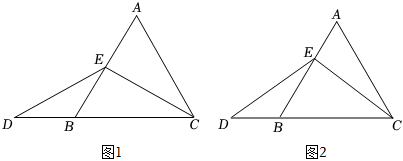
（1）特殊情况•探索结论
当点E为线段AB的中点时，如图1，确定线段AE与DB的大小关系请你直接写出结论：AE DB．（选填“＞”，“＜”或“=”）
（2）特例启发•解答题目
当E为线段AB上除中点外的任意一点时，其余条件不变，如图2，（1）中线段AE与DB的大小关系会发生改变吗？若不会，请证明；若改变，请说明理由．
（3）拓展结论•设计新题
经过以上的解答，小聪和小明发现如果把刘老师的题目稍加改变，就会得到这样一道题目：在等边△ABC中，点E在直线AB上，点D在直线BC上，且ED=EC．若△ABC的边长为1，AE=2，求CD的长．
请你根据（1）（2）的探究过程，尝试解决两人改编的此问题，直接写出CD的长．发布：2025/5/29 13:30:5组卷：223引用：5难度：0.1 -
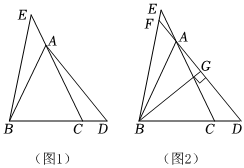3．如图，在等边△ABC中，点D、E分别在BC、CA的延长线上，AE=CD，连接BE、AD．
（1）求证：∠CAD=∠ABE；
（2）如图2，延长DA，交BE于点F，过B点作BG⊥AD于G．
①求∠EBG的大小；
②若，求此时FGEF=4的值．BEFG发布：2025/5/29 13:30:5组卷：64引用：2难度：0.5
