下面是某数学兴趣小组探究用不同方法作线段AB的垂直平分线的讨论片段，请仔细阅读，并完成相应的任务：
| 小明：如图①， （1）分别以点A、B为圆心，大于AB的长为半径作弧，两弧在AB上方交于点C，连接CA，CB； （2）以点C为圆心，小于CA的长为半径作弧，分别交AC、BC于点D、E； （3）分别以点D、E为圆心，大于 1 2 （4）作直线CP．则直线CP即为线段AB的垂直平分线． 小军；我认为小明的作图方法很有创意，但是太麻烦了，我的第（3）步改进如下： 如图②，连接BD、AE，交于点P．其它步骤与小明的完全相同．  |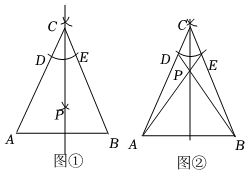
（1）小明的作图依据是
等腰三角形的三线合一
等腰三角形的三线合一
．（2）判断小军作图得到的直线CP是否是线段AB的垂直平分线？并说明理由；
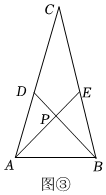
（3）如图③，已知△ABC中，CA=CB，∠ACB=30°，点D、E分别是射线CA、CB上的动点，且CD=CE，连接BD、AE，交点为P，当
AB
=
6
【考点】三角形综合题．
【答案】等腰三角形的三线合一
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/2 8:0:9组卷：323引用：3难度：0.3
相似题
-
1．如图（1），已知CA=CB，CD=CE，且∠ACB=∠DCE，将△DCE绕C点旋转（A、C、D三点在同一直线上除外）．
（1）求证：△ACD≌△BCE；
（2）在△DCE绕C点旋转的过程中，若ED、AB所在的直线交于点F，当点F为边AB的中点时，如图2所示．求证：∠ADF=∠BEF（提示：利用类倍长中线方法添加辅助线）；
（3）在（2）的条件下，求证：AD⊥CD．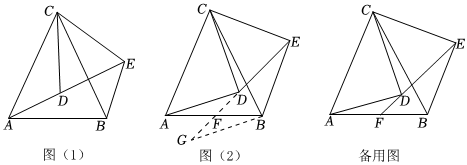
发布：2025/6/5 4:0:1组卷：1141引用：12难度：0.3 -
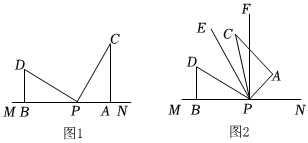2．如图，两个形状、大小完全相同的含有30°、60°的三角板如图放置，PA、PB与直线MN重合，且三角板PAC，三角板PBD均可以绕点P逆时针旋转，我们规定，如果两个三角形只要有一组边平行，我们就称这两个三角形为“孪生三角形”．
（1）如图1，∠DPC=度；
（2）如图2，三角板BPD不动，三角板PAC从PN处开始绕点P逆时针旋转（0°＜旋转角＜180°），若PF平分∠APD，PE平分∠CPD，求∠EPF的度数；
（3）在（2）的条件下，若三角板PAC的旋转速度每秒10°，设旋转时间为t秒，问t为何值时，问这两个三角形是“孪生三角形”．发布：2025/6/5 9:0:1组卷：66引用：1难度：0.2 -
3．如图，△ABC为等边三角形，直线l经过点C，在l上位于C点右侧的点D满足∠BDC=60°．
（1）如图1，在l上位于C点左侧取一点E，使∠AEC=60°，求证：△AEC≌△CDB；
（2）如图2，点F、G在直线l上，连接AF，在l上方作∠AFH=120°，且AF=HF，∠HGF=120°，求证：HG+BD=CF；
（3）在（2）的条件下，当A、B位于直线l两侧，其余条件不变时（如图3），线段HG、CF、BD的数量关系为．
发布：2025/6/5 5:0:1组卷：2123引用：6难度：0.1
