实践探究：
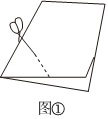
如图，把一个长方形的纸片对折两次，然后剪下一个角，若得到一个正方形，剪口与折痕应成 4545度的角．
知识应用：
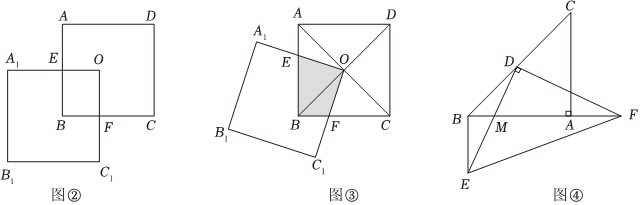
（1）小明按照以上方法剪出两个边长为1的全等正方形，如图②所示摆放，则四边形OEBF的面积为 1414．
（2）小明发现，正方形A1B1C1O在绕点O转动的过程中，两个正方形重叠部分的面积与正方形ABCD面积之间存在一定的数量关系，如图③写出该数量关系，并予以证明．
拓展延伸：
小明剪了两个大小不同的等腰直角三角形ABC和等腰直角三角形DEF，且∠BAC=∠EDF=90°，如图④放置，其中点D是BC的中点，点F在BA的延长线上，BE∥AC，当点M是DE的中点，EF=10时，请直接写出两个等腰直角三角形重叠部分的面积．
1
4
1
4
10
【考点】四边形综合题．
【答案】45；
1
4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/6 8:0:9组卷：234引用：4难度：0.3
相似题
-
1．如图，矩形ABCD中，AB=4，AD=3，点E在折线BCD上运动，将AE绕点A顺时针旋转得到AF，旋转角等于∠BAC，连接CF．
（1）当点E在BC上时，作FM⊥AC，垂足为M，求证：AM=AB；
（2）当AE=3时，求CF的长；2
（3）连接DF，点E从点B运动到点D的过程中，试探究DF的最小值．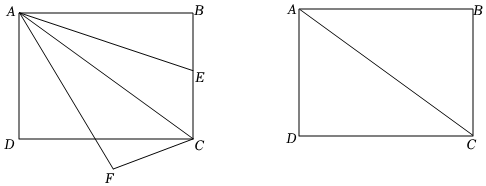
发布：2025/6/10 11:30:1组卷：3953引用：8难度：0.1 -
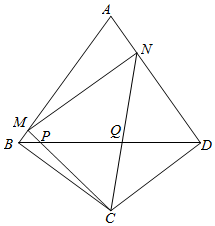2．如图，四边形ABCD中，AB=AD=4，CB=CD=3，∠ABC=∠ADC=90°，点M、N是边AB、AD上的动点，且∠MCN=∠BCD，CM、CN与对角线BD分别交于点P、Q．12
（1）求sin∠MCN的值；
（2）当DN=DC时，求∠CNM的度数；
（3）试问：在点M、N的运动过程中，线段的比值是否发生变化？如不变，请求出这个值；如变化，请至少给出两个可能的值，并说明点N相应的位置．PQMN发布：2025/6/10 13:0:2组卷：1113引用：6难度：0.1 -
3．如图，在矩形ABCD中，E是BC上一动点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G，AB=3，AD=4．
（1）如图1，当∠DAG=30°时，求BE的长；
（2）如图2，当点E是BC的中点时，求线段GC的长；
（3）如图3，点E在运动过程中，当△CFE的周长最小时，直接写出BE的长．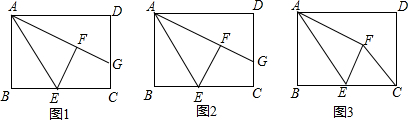
发布：2025/6/10 12:30:1组卷：1237引用：11难度：0.3
