我们可以利用解二元一次方程组的代入消元法解形如x2+y2=10① 2x-y=5 ②
的二元二次方程组,实质是将二元二次方程组转化为一元一次方程或一元二次方程来求解.其解法如下:
解:由②得y=2x-5,③
将③代入①得x2+(2x-5)2=10,
整理得x2-4x+3=0,解得x1=1,x2=3.
将x1=1,x2=3代入③得y1=1×2-5=-3,y2=2×3-5=1.
所以原方程组的解为x1=1, y1=-3,
x2=3, y2=1,
(1)请你用代入消元法解二元二次方程组:2x-y=3,① y2-4x2+6x-3=0;②
(2)若关于x,y的二元二次方程组2x+y=1,① ax2+y2+2x+1=0②
有两组不同的实数解,求实数a的取值范围.
x 2 + y 2 = 10 ① |
2 x - y = 5 ② |
x 1 = 1 , |
y 1 = - 3 , |
x 2 = 3 , |
y 2 = 1 , |
2 x - y = 3 , ① |
y 2 - 4 x 2 + 6 x - 3 = 0 ; ② |
2 x + y = 1 , ① |
a x 2 + y 2 + 2 x + 1 = 0 ② |
【答案】(1)
;
(2)(-∞,-4)∪(-4,-).
x = 1 |
y = - 1 |
(2)(-∞,-4)∪(-4,-
7
2
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/8/12 11:0:3组卷:11引用:1难度:0.5
相似题
-
1.已知
tan(x+π4)=1+tanx1-tanx,那么函数y=tanx的周期为π.类比可推出:已知x∈R且(x≠kπ+π4),那么函数y=f(x)的周期是( )f(x+π)=1+f(x)1-f(x)发布:2025/1/6 8:0:1组卷:11引用:1难度:0.7 -
2.阅读下表后,请应用类比的思想,得出椭圆中的结论:
圆 椭圆 定
义平面上到动点P到定点O的距离等于定长的点的轨迹 平面上的动点P到两定点F1,F2的距离之和等于定值2a的点的轨迹(2a>|F1F2|) 结
论如图,AB是圆O的直径,直线AC,BD是圆O过A,B的切线,P是圆O上任意一点,
CD是过P的切线,则有“PO2=PC•PD”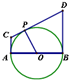
椭圆的长轴为AB,O是椭圆的中心,F1,F2是椭圆的焦点,直线AC,BD是椭圆过A,B的切线,P是椭圆上任意一点,CD是过P的切线,则有 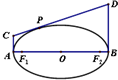 发布:2025/1/28 8:0:2组卷:32引用:2难度:0.5
发布:2025/1/28 8:0:2组卷:32引用:2难度:0.5 -
3.若
,x≠kπ+π4,则y=tanx的周期为π.类比可推出:设x∈R且tan(x+π4)=1+tanx1-tanx,则y=f(x)的周期是( )f(x+π)=1+f(x)1-f(x)发布:2025/1/6 8:0:1组卷:36引用:1难度:0.5


