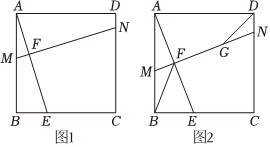
如图1，在正方形ABCD中，点E为BC边上任意一点（点E不与B，C重合），点F在线段AE上，过点F的直线MN⊥AE，分别交AB，CD于点M，N．
（1）直接写出：∠AMN与∠AEB的数量关系：∠AEB=∠AMN∠AEB=∠AMN；AE与MN之间数量关系：AE=MNAE=MN；
（2）如图2：当点F为AE中点时，其他条件不变，连接正方形的对角线BD，MN与BD交于点G，连接BF，求证：BF=FG．
【考点】正方形的性质；全等三角形的判定与性质．
【答案】∠AEB=∠AMN；AE=MN
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/4 8:0:9组卷：135引用：2难度：0.5
相似题
-
1．已知正方形ABCD，以CD为边作等边△CDE，则∠AED的度数是 ．
发布：2025/6/8 22:0:1组卷：783引用：48难度：0.5 -
2．正方形ABCD，正方形CEFG如图放置，点B、C、E在同一条直线上，点P在BC边上，PA=PF，且∠APF=90°，连接AF交CD于点M．有下列结论：①EC=BP；②AP=AM；③∠BAP=∠GFP；④AB2+CE2=AF2；⑤S正方形ABCD+S正方形CGFE=2S△APF，其中正确的是（ ）12发布：2025/6/8 21:0:2组卷：1297引用：12难度：0.7 -
3．正方形ABCD中，M为射线CD上一点（不与D重合），以CM为边，在正方形ABCD的异侧作正方形CFGM，连接BM，DF，直线BM与DF交于点E．
（1）如图1，若M在CD的延长线上，求证：DF=BM，DF⊥BM；
（2）如图2，若M移到边CD上．
①在（1）中结论是否仍成立？（直接回答不需证明）
②连接BD，若BD=BF，且正方形CFGM的边长为1，试求正方形ABCD的周长．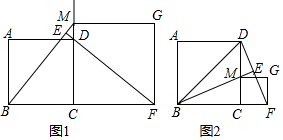
发布：2025/6/9 0:0:2组卷：1405引用：5难度：0.4
