综合与实践
问题背景：
（1）已知A（1，2），B（3，2），C（1，-1），D（-3，-3）．在平面直角坐标系中描出这几个点，并分别找到线段AB和CD中点P1、P2，然后写出它们的坐标，则P1（2，2）（2，2），P2（-1，-2）（-1，-2）．
探究发现：
（2）结合上述计算结果，你能发现若线段的两个端点的坐标分别为（x1，y1），（x2，y2），则线段的中点坐标为（x1+x22，y1+y22）（x1+x22，y1+y22）．
拓展应用：
（3）利用上述规律解决下列问题：已知三点E（-1，2），F（3，1），G（1，4），第四个点H（x,y）与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合，求点H的坐标．
（
x
1
+
x
2
2
，
y
1
+
y
2
2
）
（
x
1
+
x
2
2
，
y
1
+
y
2
2
）
【考点】规律型：点的坐标．
【答案】（2，2）；（-1，-2）；
（
x
1
+
x
2
2
，
y
1
+
y
2
2
）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/14 8:0:9组卷：2649引用：13难度：0.5
相似题
-
1．在平面直角坐标系xOy中，对于点P（x,y）我们把点P（-y+1，x+1）叫做点P的伴随点．已知点A1的伴随点为A2，点A2的伴随点为A3，点A3的伴随点为A4，…这样依次得到点A1，A2，A3，…，An，…．若点A1的坐标为（2，4），点A2022的坐标为（ ）
发布：2025/6/8 7:30:1组卷：163引用：1难度：0.5 -
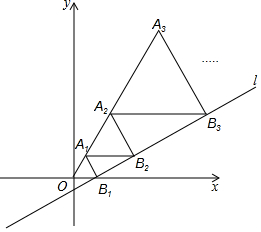2．如图，在平面直角坐标系中，直线l：y=x-33与x轴交于点B1，以OB1为边长作等边三角形A1OB1，过点A1作A1B2平行于x轴，交直线l于点B2，以A1B2为边长作等边三角形A2A1B2，过点A2作A2B3平行于x轴，交直线l于点B3，以A2B3为边长作等边三角形A3A2B3，…，则点A2021的横坐标是 ．33发布：2025/6/8 7:30:1组卷：404引用：5难度：0.6 -
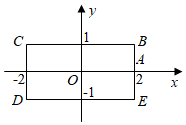3．如图，长方形BCDE的各边分别平行于x轴与y轴，物体甲和物体乙由点A（2，0）同时出发，沿长方形BCDE的边做环绕运动，物体甲按逆时针方向以1个单位长度/秒的速度匀速运动，物体乙按顺时针方向以2个单位长度/秒的速度匀速运动，则两个物体运动后的第2022次相遇地点的坐标是（ ）发布：2025/6/8 8:0:6组卷：328引用：5难度：0.6
