综合与实践
数学是以数量关系和空间形式为主要研究对象的科学，数学实践活动有利于我们在图形运动变化的过程中去发现其中的位置关系和数量关系，让我们在学习与探索中发现数学的美，体会数学实践活动带给我们的乐趣．
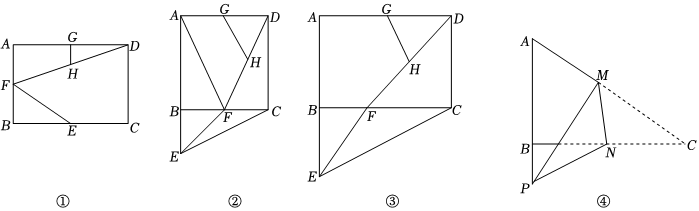
转一转：如图①，在矩形ABCD中，点E、F、G分别为边BC、AB、AD的中点，连接EF、DF，H为DF的中点，连接GH，将△BEF绕点B旋转，线段DF、GH和CE的位置和长度也随之变化．当△BEF绕点B顺时针旋转90°时，请解决下列问题：
（1）图②中，AB=BC，此时点E落在AB的延长线上，点F落在线段BC上，连接AF，猜想GH与CE之间的数量关系，并证明你的猜想；
（2）图③中，AB=2，BC=3，则GHCE=1313，请证明你的结论；
（3）当AB=m,BC=n时，GHCE=m2nm2n；
剪一剪、折一折：
（4）在（2）的条件下，连接图③中矩形的对角线AC，并沿对角线AC剪开，得△ABC（如图④）点M、N分别在AC、BC上，连接MN，将△CMN沿MN翻折，使点C的对应点P落在AB的延长线上，若PM平分∠APN，则CM长为 31353135．
GH
CE
1
3
1
3
GH
CE
m
2
n
m
2
n
3
13
5
3
13
5
【考点】相似形综合题．
【答案】；；
1
3
m
2
n
3
13
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/29 8:0:10组卷：457引用：2难度：0.1
相似题
-
1．在Rt△ABC中，∠BAC=90°，AB=AC，在Rt△ADE中，∠DAE=90°，2AD=AB，2AE=AC，连接DE，AN⊥BC，垂足为N，AM⊥DE，垂足为M．
（1）观察猜想
图①中，点D，E分别在AB，AC上时，的值为 ；BDCE的值为 ．BDMN
（2）探究证明
如图②，将△ADE绕点A顺时针旋转，旋转角为α（0°＜α＜360°），连接BD，CE，判断问题（1）中的数量关系是否仍然存在，并证明；
（3）拓展延伸
在△ADE旋转的过程中，设直线CE与BD相交于点F，若∠CAE=90°，AB=6，请直接写出线段BF的长．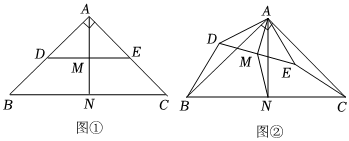
发布：2025/5/23 17:0:1组卷：518引用：1难度：0.1 -
2．【实践操作】：
第一步：如图①，将矩形纸片ABCD沿过点D的直线折叠，使点A落在CD上的A'处，得到折痕DE，然后把纸片展平．
第二步：如图②，将图中的矩形纸片ABCD沿过点E的直线折叠，点C恰好落在AD上的点C'处，点B落在B'处，得到折痕EF，B'C'交AB于点M，C'F交DE于点N，再把纸片展平．
【问题解决】：
（1）如图①，四边形AEA'D的形状是 ；
（2）如图②，线段MC'与ME是否相等？若相等，请给出证明；若不相等，请说明理由；
（3）如图②，若AC'=3cm,DC'=6cm,则MC'=，=．DNEN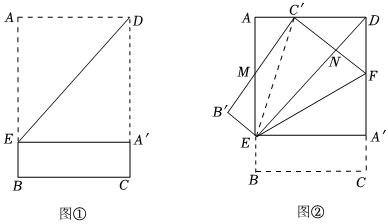
发布：2025/5/23 19:0:2组卷：311引用：3难度：0.1 -
3．问题提出
（1）如图①，在△ABC中，点D、E、F分别为边AB、AC、BC的中点，DE∥BC，BC=8，AF交DE于点G，则DG的长为 ；
问题探究
（2）如图②，在等腰直角△ABC中，∠C=90°，AC=4，点D为线段CB上一动点（点D不与点B、C重合），以AD为腰且在AD的右侧作等腰直角△ADF，∠ADF=90°，AB与FD交于点E，连接BF，求证：△ACD∽△ABF；
问题解决
（3）如图是郊外一空地，为了美化生态环境，现要将这块地打造成一个公园，在空地一侧挖一个四边形的人工湖CDQP，点P、Q分别在边AB、AD上，且满足PB=AQ，已知AB=AD，∠ACB=∠BAD=90°，AB=500m,BC=300m,为了满足湖周边的建设用地需要，人工湖的面积需尽可能小，设PB的长为x（m），四边形CDQP的面积为S（m2）．
①求S与x之间的函数关系式；
②求人工湖面积的最小值及此时AQ的长．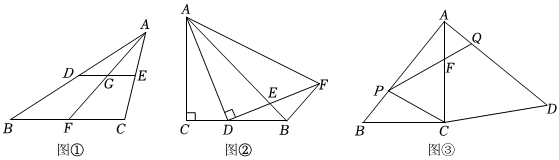
发布：2025/5/23 16:0:1组卷：259引用：1难度：0.3
相关试卷
