当前位置：
章节挑题
请展开查看知识点列表
>
更多>>
|
原创
已完结
|
知识图解
新知探究
答疑解惑
针对训练
浏览次数：4710
更新：2025年06月09日
|
|
原创
已完结
|
知识图解
新知探究
答疑解惑
针对训练
浏览次数：7020
更新：2025年06月09日
|
2961．如图，抛物线y=-x2+2x+c与x轴交于A，B两点，它的对称轴与x轴交于点N，过顶点M作ME⊥y轴于点E，连接BE交MN于点F，已知点A的坐标为（-1，0）．
（1）求该抛物线的解析式及顶点M的坐标．
（2）求△EMF与△BNF的面积之比．发布：2024/6/27 10:35:59组卷：2109引用：64难度：0.3
2962．如图，蜂巢的横截面由正六边形组成，且能无限无缝隙拼接，称横截面图形由全等正多边形组成，且能无限无缝隙拼接的多边形具有同形结构．
若已知具有同形结构的正n边形的每个内角度数为α，满足：360=kα（k为正整数），多边形外角和为360°，则k关于边数n的函数是（写出n的取值范围）发布：2024/6/27 10:35:59组卷：447引用：23难度：0.72963．已知点A（-2，n）在抛物线y=x2+bx+c上．
（1）若b=1，c=3，求n的值；
（2）若此抛物线经过点B（4，n），且二次函数y=x2+bx+c的最小值是-4，请画出点P（x-1，x2+bx+c）的纵坐标随横坐标变化的图象，并说明理由．发布：2024/6/27 10:35:59组卷：5027引用：58难度：0.5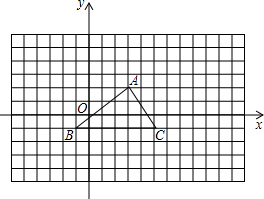
2964．如图所示的网格中，每个小方格都是边长为1的正方形，B点的坐标为（-1，-1）．
（1）把格点△ABC绕点B按逆时针方向旋转90°后得到△A1BC1，请画出△A1BC1，并写出点A1的坐标；
（2）以点A为位似中心放大△ABC，得到△AB2C2，使放大前后的面积之比为1：4请在下面网格内画出△AB2C2．发布：2024/6/27 10:35:59组卷：81引用：5难度：0.52965．阳光小区附近有一块长100m,宽80m的长方形空地，在空地上有两条相同宽度的步道（一纵一横）和一个边长为步道宽度7倍的正方形休闲广场，两条步道的总面积与正方形休闲广场的面积相等，如图1所示，设步道的宽为a（m）．
（1）求步道的宽；
（2）为了方便市民进行跑步健身，现按如图2所示方案增建塑胶跑道．已知塑胶跑道的宽为1m,长方形区域甲的面积比长方形区域乙大441m2，且区域丙为正方形，求塑胶跑道的总面积．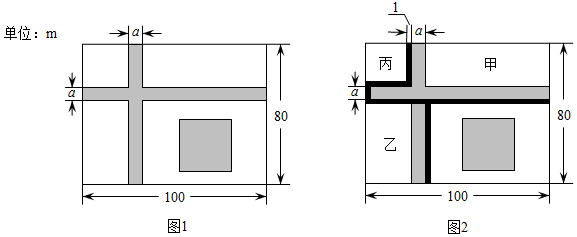
发布：2024/6/27 10:35:59组卷：1175引用：9难度：0.5
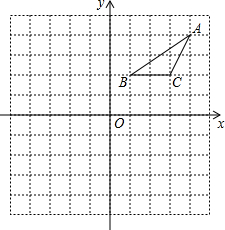2966．在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上，A的坐标是（4，4），请回答下列问题：
（1）将△ABC向下平移六个单位长度，画出平移后的△A1B1C1，并写出点A的对应点A1的坐标；
（2）画出△ABC关于原点O对称的△A2B2C2，并写出点A2的坐标；
（3）判断△A1B1C1与△A2B2C2是否关于某点成中心对称；若是，请画出对称中心M，并写出点M的坐标发布：2024/6/27 10:35:59组卷：456引用：7难度：0.5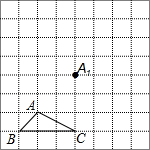
2967．如图所示，正方形网格中，△ABC为格点三角形（即三角形的顶点都在格点上）：
①把△ABC沿BA方向平移，请在网格中画出当点A移动到点A1时的△A1B1C1；
②把△A1B1C1绕点A1按逆时针方向旋转90°后得到△A2B2C2，如果网格中小正方形的边长为1，求点B1旋转到B2的路径长．发布：2024/6/27 10:35:59组卷：630引用：7难度：0.5
2968．如图，在△ABC中，AB=AC，以AB为直径作半圆⊙O，交BC于点D，连接AD，过点D作DE⊥AC，垂足为点E，交AB的延长线于点F．
（1）求证：EF是⊙O的切线．
（2）如果⊙O的半径为5，sin∠ADE=，求BF的长．45发布：2024/6/27 10:35:59组卷：3359引用：80难度：0.5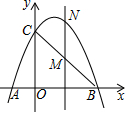
2969．如图，已知抛物线经过点A（-1，0），B（3，0），C（0，3）三点．
（1）求此抛物线的解析式；
（2）若点M是线段BC上的点（不与B，C重合），过M作NM∥y轴交抛物线于N，设点M的横坐标为m,请用含m的代数式表示MN的长；
（3）在（2）的条件下，连接NB，NC，是否存在点M，使△BNC的面积最大？若存在，求m的值；若不存在，请说明理由．发布：2024/6/27 10:35:59组卷：1234引用：10难度：0.32970．如图①，一个横截面为抛物线形的隧道，其底部的宽AB为8m,拱高为4m,该隧道为双向车道，且两车道之间有0.4m的隔离带，一辆宽为2m的货车要安全通过这条隧道，需保持其顶部与隧道间有不少于0.5m的空隙，按如图②所建立平面直角坐标系．
（1）求该抛物线对应的函数关系式；
（2）通过计算说明该货车能安全通过的最大高度．
发布：2024/6/27 10:35:59组卷：1698引用：8难度：0.5
