高中数学知识点总结_高中数学知识点试题

当前位置：知识点挑题

请展开查看知识点列表

预备知识
函数
几何与代数
概率与统计
数学知识的延伸

更多>>

原创

更新中

【优学堂】2026年高考数学一轮复习

明确考点剖析考向配加典例和变式题真题演练及精选模拟全方位助力备考

浏览次数：3536 更新：2025年06月20日

原创

更新中

《黄金讲练》2025-2026学年人教A版（2019）必修第一册高一同步课堂

知识图解新知探究答疑解惑针对训练

浏览次数：485 更新：2025年06月20日

2241．已知非零向量
a
，
b
，
c
，那么“
a
=
b
”是“
a
•
c
=
b
•
c
”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
发布：2024/12/28 23:30:2组卷：192引用：8难度：0.9
解析

2242．甲，乙两个工人在同样的条件下生产，日产量相等，每天出废品的情况如下表所列，则有结论：（　　）

工人甲乙

废品数 0 1 2 3 0 1 2 3

概率 0.4 0.3 0.2 0.1 0.3 0.5 0.2 0

A．甲的产品质量比乙的产品质量好一些

B．乙的产品质量比甲的产品质量好一些

C．两人的产品质量一样好

D．无法判断谁的质量好一些

发布：2024/12/28 23:30:2组卷：93引用：11难度：0.9

解析

2243．已知函数
f
（
x
）
=
2
sin
（
2
x
-
π
3
）
，则它的单调递增区间为
．
发布：2024/12/28 23:30:2组卷：92引用：2难度：0.8
解析
2244．设函数f（x）=e^x-ax-1．
（1）若函数f（x）在R上单调递增，求a的取值范围；
（2）当a＞0时，设函数f（x）的最小值为g（a），求证：g（a）≤0．
发布：2024/12/28 23:30:2组卷：25引用：4难度：0.5
解析

2245．手机完全充满电量，在开机不使用的状态下，电池靠自身消耗一直到出现低电量警告之间所能维持的时间称为手机的待机时间．为了解A，B两个不同型号手机的待机时间，现从某卖场库存手机中随机抽取A，B两个型号的手机各5台，在相同条件下进行测试，统计结果如下：

手机编号 1 2 3 4 5

A型待机时间（h） 120 125 122 124 124

B型待机时间（h） 118 123 127 120 a

已知A，B两个型号被测试手机待机时间的平均值相等．
（Ⅰ）求a的值；
（Ⅱ）判断A，B两个型号被测试手机待机时间方差的大小（结论不要求证明）；
（Ⅲ）从被测试的手机中随机抽取A，B型号手机各1台，求至少有1台的待机时间超过122小时的概率．
（注：n个数据x₁，x₂，…，x_n的方差s²=
1
n
[（x₁-
x
）²+（x₂-
x
）²+…+（x_n-
x
）²]，其中
x
为数据x₁，x₂，…，x_n的平均数）

发布：2024/12/28 23:30:2组卷：216引用：4难度：0.3

解析

2246．已知在△ABC中，a,b,c分别是角A，B，C所对的边，且
cos
A
（
3
sin
A
-
cos
A
）
=
1
2
．
（1）求角A的大小．
（2）若
a
=
2
2
，
S
△
ABC
=
2
3
，判断三角形的形状．
发布：2024/12/28 23:30:2组卷：65引用：2难度：0.6
解析
2247．设函数f（x）=e^x（x-1），函数g（x）=mx-m（m＞0），若对任意的x₁∈[-2，2]，总存在x₂∈[-2，2]，使得f（x₁）=g（x₂），则实数m的取值范围是
发布：2024/12/28 23:30:2组卷：101引用：3难度：0.5
解析
2248．已知
z
+
i
z
-
i
=
2
i
（i为虚数单位），则
z
=（　　）
A．
4
5
+
3
5
i B．
3
5
+
4
5
i C．
3
5
+
4
5
i D．
4
5
-
3
5
i
发布：2024/12/28 23:30:2组卷：88引用：4难度：0.8
解析
2249．对于数列{a_n}，把a₁作为新数列{b_n}的第一项，把a_i或-a_i（i=2，3，4，…，n）作为新数列{b_n}的第i项，数列{b_n}称为数列{a_n}的一个生成数列．例如，数列1，2，3，4，5的一个生成数列是1，-2，-3，4，5．已知数列{b_n}为数列{
1
2
n
}（n∈N^*）的生成数列，S_n为数列{b_n}的前n项和．
（Ⅰ）写出S₃的所有可能值；
（Ⅱ）若生成数列{b_n}满足S_3n=
1
7
（1-
1
8
n
），求数列{b_n}的通项公式；
（Ⅲ）证明：对于给定的n∈N^*，S_n的所有可能值组成的集合为{x|x=
2
k
-
1
2
n
，k∈N^*，k≤2^n-1}．
发布：2024/12/28 23:30:2组卷：124引用：6难度：0.1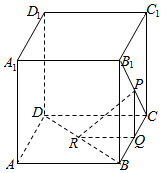
解析
2250．如图，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，P是B₁C的中点，Q，R分别在BC，BD上，则△PQR周长的最小值为
．
发布：2024/12/28 23:30:2组卷：125引用：4难度：0.5
解析

首页上一页 …225 226 227 228 …下一页尾页

A．充分不必要条件	B．必要不充分条件
C．充要条件	D．既不充分也不必要条件

手机编号	1	2	3	4	5
A型待机时间（h）	120	125	122	124	124
B型待机时间（h）	118	123	127	120	a

2241．已知非零向量a，b，c，那么“a=b”是“a•c=b•c”的（ ）

2242．甲，乙两个工人在同样的条件下生产，日产量相等，每天出废品的情况如下表所列，则有结论：（ ） 工人 甲 乙 废品数 0 1 2 3 0 1 2 3 概率 0.4 0.3 0.2 0.1 0.3 0.5 0.2 0

2243．已知函数f（x）=2sin（2x-π3），则它的单调递增区间为 ．

2244．设函数f（x）=ex-ax-1．（1）若函数f（x）在R上单调递增，求a的取值范围；（2）当a＞0时，设函数f（x）的最小值为g（a），求证：g（a）≤0．

2246．已知在△ABC中，a,b,c分别是角A，B，C所对的边，且cosA（3sinA-cosA）=12．（1）求角A的大小．（2）若a=22，S△ABC=23，判断三角形的形状．

2247．设函数f（x）=ex（x-1），函数g（x）=mx-m（m＞0），若对任意的x1∈[-2，2]，总存在x2∈[-2，2]，使得f（x1）=g（x2），则实数m的取值范围是

2248．已知z+iz-i=2i（i为虚数单位），则z=（ ）

2250．如图，在棱长为2的正方体ABCD-A1B1C1D1中，P是B1C的中点，Q，R分别在BC，BD上，则△PQR周长的最小值为 ．

2241．已知非零向量
a
，
b
，
c
，那么“
a
=
b
”是“
a
•
c
=
b
•
c
”的（　　）

2242．甲，乙两个工人在同样的条件下生产，日产量相等，每天出废品的情况如下表所列，则有结论：（　　）

工人甲乙

废品数 0 1 2 3 0 1 2 3

概率 0.4 0.3 0.2 0.1 0.3 0.5 0.2 0

2243．已知函数
f
（
x
）
=
2
sin
（
2
x
-
π
3
）
，则它的单调递增区间为
．

2244．设函数f（x）=e^x-ax-1．
（1）若函数f（x）在R上单调递增，求a的取值范围；
（2）当a＞0时，设函数f（x）的最小值为g（a），求证：g（a）≤0．

2246．已知在△ABC中，a,b,c分别是角A，B，C所对的边，且
cos
A
（
3
sin
A
-
cos
A
）
=
1
2
．
（1）求角A的大小．
（2）若
a
=
2
2
，
S
△
ABC
=
2
3
，判断三角形的形状．

2247．设函数f（x）=e^x（x-1），函数g（x）=mx-m（m＞0），若对任意的x₁∈[-2，2]，总存在x₂∈[-2，2]，使得f（x₁）=g（x₂），则实数m的取值范围是

2248．已知
z
+
i
z
-
i
=
2
i
（i为虚数单位），则
z
=（　　）

2250．如图，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，P是B₁C的中点，Q，R分别在BC，BD上，则△PQR周长的最小值为
．