某数学活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：
【操作发现】
（1）如图①，在△ABC中，D，E，F分别是三边的中点，连接DE，DF，他们发现∠DEC=∠DFC，请证明该结论；
【数学思考】
（2）如图②，在△ABC中，AC=BC，D是AB的中点，分别以AC和BC为斜边，向△ABC的外侧作两个等腰直角三角形△ACE和△BCF，连接DE，DF，他们发现DE=DF，请证明该结论；
【类比探索】
（3）如图，在△ABC中，D，E，F分别是三边的中点，分别以BC和AC为斜边，向△ABC的内侧作等腰直角三角形△BCH和△ACG，连接DE，DF，DG，DH，试猜想线段DG和DH的关系，并证明你的猜想．
【考点】三角形综合题．
【答案】（1）证明见解答；
（2）证明见解答；
（3）DH=DG，DH⊥DG，理由见解答．
（2）证明见解答；
（3）DH=DG，DH⊥DG，理由见解答．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/11 8:0:9组卷：87引用：1难度：0.1
相似题
-
1．【回顾思考】：用数学的思维思考
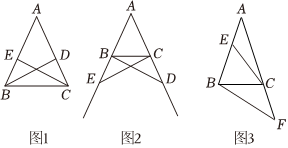
（1）如图1，在△ABC中，AB=AC．
①若BD，CE是△ABC的角平分线．求证：BD=CE．
②若点D，E分别是边AC，AB的中点，连接BD，CE．求证：BD=CE．
（从①②两题中选择一题加以证明）
（2）【猜想证明】：用数学的眼光观察
经过做题反思，小明同学认为：在△ABC中，AB=AC，D为边AC上一动点（不与点A，C重合）对于点D在边AC上的任意位置，在另一边AB上总能找到一个与其对应的点E，使得BD=CE．进而提出问题：若点D，E分别运动到边AC，AB的延长线上，BD与CE还相等吗？请解决下面的问题：
如图2，在△ABC中，AB=AC，点D，E分别在边AC，AB的延长线上，请添加一个条件（不再添加新的字母），使BD=CE，并证明．
（3）【拓展探究】：用数学的语言表达
如图3，在△ABC中，AB=AC=3，∠A=36°，E为边AB上任意一点（不与点A，B重合），F为边AC延长线上一点．判断BF与CE能否相等．若能，求CF的取值范围；若不能，说明理由．发布：2025/5/21 17:0:2组卷：305引用：1难度：0.1 -
2．如图a和图b,在△ABC中，AB=AC，BC=8，tanC=
．点K在AC边上，点M，N分别在AB，BC上，且AM=CN=2．点P从点M出发沿折线匀速移动，到达点N时停止；而点Q在AC边上随P移动，且始终保持∠APQ=∠B．34
（1）当点P在BC上时，求点P与点A的最短距离：
（2）若点P在MB上，且PO将△ABC的面积分成上下4：5两部分时，求MP的长；
（3）设点P移动的路程为x,当0≤x≤3及3≤x≤9时，分别求点P到直线AC的距离（用含x的式子表示）；
（4）在点P处设计并安装一扫描器，按定角∠APQ扫描△APQ区域（含边界），扫描器随点P从M到B再到N共用时36秒．若AK=，请直接写出点K被扫描到的总时长．94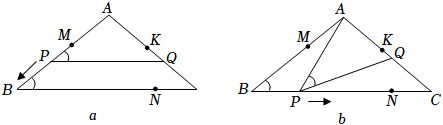
发布：2025/5/21 18:0:1组卷：138引用：1难度：0.2 -
3．【初步感知】（1）如图1，点A，B，C，D均在小正方形网格的格点上，则
=；tan∠BAC2
【问题解决】（2）求tan15°的值；
方案①：如图2，在△ABC中，∠C=90°，∠BAC=30°，作AD平分∠BAC交BC于D；…
方案②：如图3，在△ABC中，AB=AC，∠A=30°，过点B作BD⊥AC，垂足为D；…
请你选择其中一种方案求出tan15°的值（结果保留根号）；
【思维提升】（3）求sin18°的值；如图4，在△ABC中，AB=AC，∠A=36°．求sin18°的值（结果保留根号）．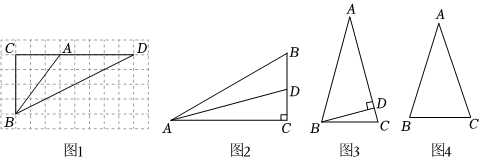
发布：2025/5/21 20:30:1组卷：350引用：4难度：0.1
