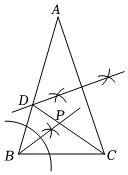
如图，在△ABC中，AB=AC，∠A=40°，点D，P分别是图中所作直线和射线与AB，CD的交点．根据图中尺规作图痕迹推断，以下结论错误的是（ ）
【答案】D
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/3 8:0:9组卷：1074引用：17难度：0.5
相似题
-
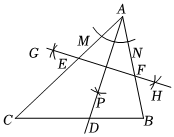1．如图，已知△ABC．以点A为圆心，以适当长为半径画弧，交AC于点M，交AB于点N．分别以M，N为圆心，以大于MN的长为半径画弧，两弧在∠BAC的内部相交于点P．作射线AP交BC于点D．分别以A，D为圆心，以大于12AD的长为半径画弧，两弧相交于G，H两点．作直线GH，交AC，AB分别于点E，F．根据以上作图，若AF=2，CE=3，BD=12，则CD的长是 ．53发布：2025/5/24 17:30:1组卷：50引用：2难度：0.7 -
2．下面是小立设计的“过圆上一点作这个圆的切线”的尺规作图过程．
已知：⊙O及圆上一点A．
求作：直线AB，使得AB为⊙O的切线，A为切点．
作法：如图2，
①连接OA并延长到点C；
②分别以点A，C为圆心，大于长为半径作弧，两弧交于点D（点D在直线OA上方）；12AC
③以点D为圆心，DA长为半径作⊙D；
④连接CD并延长，交⊙D于点B，作直线AB．
直线AB就是所求作的直线．
根据小立设计的尺规作图过程，完成下面的证明．（说明：括号里填推理的依据）
证明：连接AD．
∵=AD
∴点C在⊙D上，
∴CB是⊙D的直径．
∴=90°．（ ）
∴AB⊥．
∵OA是⊙O的半径，
∴AB是⊙O的切线．（ ）发布：2025/5/24 14:0:2组卷：475引用：10难度：0.5 -
3．如图：已知：点P和直线m.
求作：以点P为直角顶点的等腰直角三角形，使它的斜边落在直线m上，并在三角形内部做出以斜边中点为圆心的面积最大的半圆O．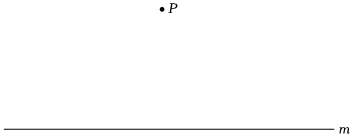
结论：发布：2025/5/24 16:0:1组卷：109引用：3难度：0.7
