已知正方形ABCD的边长为6，动点E，F分别在边AB，CD上运动，连接EF．
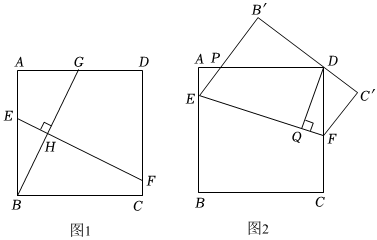
（1）如图1，过B作BG⊥EF交边AD于点G，交EF于点H．
i）若G为AD的中点，H为BG的中点，求AE的长；
ⅱ）探索线段AE，DG，CF之间的数量关系，写出你的结论并证明．
（2）如图2，将四边形EBCF沿EF翻折得到四边形EB′C′F，B′E与AD相交于点P，调整点E和点F的位置使得线段B′C′始终经过顶点D．
i）若点D到EF的距离DQ=10，求DP的长；
ⅱ）点B′到AD的距离是否存在最大值？若存在，请直接写出这个最大距离；若不存在，请说明理由．
DQ
=
10
【考点】四边形综合题．
【答案】（1）i）；ⅱ）GD=AE+CF，理由见解析；
（2）i）5；ⅱ）点B′到AD的距离的最大值为．
9
4
（2）i）5；ⅱ）点B′到AD的距离的最大值为
6
2
-
6
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 8:0:10组卷：378引用：2难度：0.1
相似题
-
1．如图1，矩形ABCD中，AB=15，BC=20，将矩形ABCD绕着点A顺时针旋转，得到矩形BEFG．
（1）当点E落在BD上时，则线段DE的长度等于 ；
（2）如图2，当点E落在AC上时，求△BCE的面积；
（3）如图3，连接AE、CE、AG、CG，判断线段AE与CG的位置关系且说明理由，并求CE2+AG2的值；
（4）在旋转过程中，请直接写出S△BCE+S△ABG的最大值．发布：2025/6/9 10:0:1组卷：350引用：3难度：0.2 -
2．如图1，在平面直角坐标系中，A（-4，-1），B（2，-1），将线段AB向上平移4个单位至线段CD，使A的对应点为C，B的对应点为D．CD与y轴交于E．
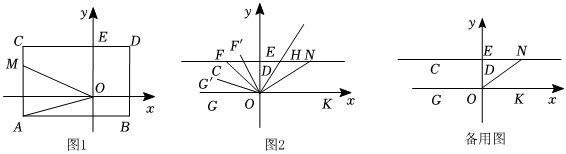
（1）直接写出点C，D的坐标．
（2）现有一动点M，从A点出发沿A→C→E路径向终点E运动，是否存在这样的点M，使点A，O，M三点围成的三角形面积等于四边形ABDC面积的，即724，若存在，请求出点M坐标，若不存在，请说明理由；S△AOM=724S四边形ABDC
（3）如图2，点G、K分别在x轴负半轴与正半轴上，直线CD上有两点F、N满足∠GOF=45°，∠NOK=30°，现将∠GOF绕点O顺时针旋转α度（0°＜α＜135°）得到∠G'OF'，∠F'OK的角平分线交直线CD于H，请求出旋转过程中满足（∠EOG'+∠NOF'）：∠OHE=5：2时α的度数．发布：2025/6/9 11:30:1组卷：199引用：3难度：0.4 -
3．如图，矩形OABC的两条边OA、OC分别在y轴和x轴上，已知点B坐标为（8，-6）．把矩形OABC沿直线DE折叠，使点C落在点A处，直线DE与OC、AC、AB的交点分别为D、F、E．
（1）线段AC=；
（2）求点D坐标及折痕DE的长；
（3）若点P在x轴上，在平面内是否存在点Q，使以P、D、E、Q为顶点的四边形是菱形？若存在，则请直接写出点Q的坐标；若不存在，请说明理由．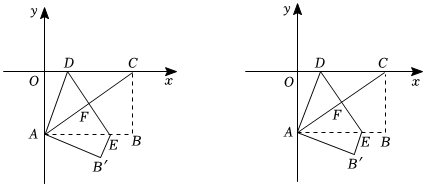
发布：2025/6/9 9:30:1组卷：171引用：1难度：0.1
