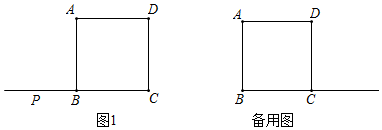
在正方形ABCD中，点P是直线BC上一点，连接AP，将线段PA绕点P顺时针旋转90°，得到线段PE，连接CE．
（1）如图1，若点P在线段CB的延长线上，过点E作EF⊥BC交BC于点H，交对角线AC于点F，连接AE
①请根据题意补全图形（不需要用尺规作图）；
②若∠PAB=20°，求∠CAE的度数；
③求证：EH=FH
（2）若点P在射线BC上，直接写出CE、CP、CD三条线段的数量关系CE=2（CD-CP）或CE=2（CD+CP）CE=2（CD-CP）或CE=2（CD+CP）．
2
2
2
2
【考点】四边形综合题．
【答案】CE=（CD-CP）或CE=（CD+CP）
2
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/6 8:0:8组卷：301引用：4难度：0.2
相似题
-
1．【问题发现】
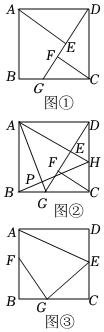
（1）如图①，在正方形ABCD中，G是BC上一点（点G与B，C不重合），AE⊥DG交DG于点E，CF⊥DG交DG于点F．试猜想线段AE，CF和EF之间的数量关系，并证明；
【延伸探究】
（2）在其余条件不变的基础上延长AE，交DC于点H，连接AG，BH，交于点P，如图②．求证：AG⊥BH；
【问题解决】
（3）如图③是一块边长为1米的正方形钢板ABCD．由于磨损，该钢板的顶点B，C，D均不能使用，王师傅计划过点A裁出一个形如四边形AEGF的零件，其中点F，E，G分别在AB，CD，BC边上，且F为AB的中点，GF⊥GE交DC于点E，连接AE，求王师傅能裁出四边形AEGF的最大面积是多少？发布：2025/5/23 8:30:2组卷：293引用：2难度：0.3 -
2．问题提出
（1）如图①，在矩形ABCD的边BC上找一点E，将矩形沿直线DE折叠，点C的对应点为C′，再在AB上找一点F，将矩形沿直线DF折叠，使点A的对应点A′落在DC上，则∠EDF=．
问题探究
（2）如图②，在矩形ABCD中，AB=10，AD=4，点P是矩形ABCD边AB上一点，连接PD、PC，将△ADP、△BCP分别沿PD、PC翻折，得到△A′DP、△B′PC，当P、A′、B′三点共线时，则称P为AB边上的“优叠点”，求此时AP的长度．
问题解决
（3）如图③，矩形ABCD位于平面直角坐标系中，AD=4，AD＜AB，点A在原点，B，D分别在x轴与y轴上，点E和点F分别是CD和BC边上的动点，运动过程中始终保持DE+BF=4．当点P是AB边上唯一的“优叠点”时，连接PE交BD于点M，连接PF交BD于点N，请问DM+BN是否能取得最大值？如果能，请确定此时点M的位置（即求出点M的坐标）及四边形ADEP的面积，若不能，请说明理由．
发布：2025/5/23 8:30:2组卷：691引用：1难度：0.1 -
3．综合与实践课上，老师让同学们以“矩形的折叠”为主题开展数学活动．
（1）操作判断
操作一：对折矩形纸片ABCD，使AD与BC重合，把纸片展平，得到折痕EF；
操作二：在AD上选一点P，沿BP折叠，使点A落在矩形内部点Q处，把纸片展平，连接PQ，BQ．根据以上操作，当点Q在EF上（如图1）时，∠QBC=°．
（2）迁移探究
小华将矩形纸片换成正方形纸片，继续探究，过程如下：
将正方形纸片ABCD按照（1）中的方式操作，并延长PQ交CD于点G，连接BG．对角线AC与BP、BG分别交于点M、N，连接PN．当点Q在EF上（如图2）时，判断线段PN与BG的位置关系，并说明理由；
（3）拓展应用
在（2）的探究中，改变点P在AD上的位置，当点G在线段FC上时（如图3），若正方形的边长为63，求S△BPG的值．，FG=3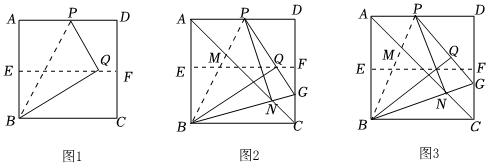
发布：2025/5/23 8:0:2组卷：358引用：1难度：0.2
