某商店出售一款商品，经市场调查反映，该商品的日销售量y（件）与销售单价x（元）之间满足一次函数关系，关于该商品的销售单价、日销售量、日销售利润的部分对应数据如下表所示．【注：日销售利润=日销售量×（销售单价-成本单价）】
| 销售单价x（元） | 75 | 78 | 82 |
| 日销售量y（件） | 150 | 120 | 80 |
| 日销售利润w（元） | 5250 | 4560 | a |
40
40
元，表中a的值是 3360
3360
．（2）求该商品日销售利润的最大值．
（3）由于某种原因，该商品进价降低了m元/件（m＞0）．该商店在今后的销售中，规定该商品的销售单价不低于68元，日销售量与销售单价仍然满足上表中的函数关系．若日销售利润最大是6820元，求m的值．
【考点】二次函数的应用．
【答案】40；3360
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/18 8:0:8组卷：53引用：2难度：0.5
相似题
-
1．【综合实践】
某公园在人工湖里安装一个喷泉，在湖心处竖直安装一根水管，在水管的顶端安一个喷水头，喷出的水柱形状可以看作是抛物线的一部分．若记水柱上某一位置与水管的水平距离为x米，与湖面的垂直高度为y米．下面的表中记录了x与y的五组数据：
（1）在下面网格（图1）中建立适当的平面直角坐标系，并根据表中所给数据画出表示y与x函数关系的图象；x（米） 0 1 2 3 4 y（米） 0.5 1.25 1.5 1.25 0.5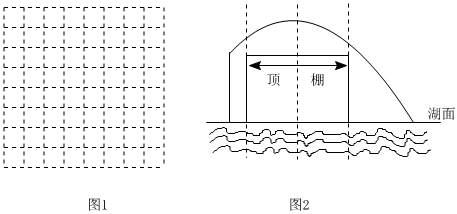 
（2）若水柱最高点距离湖面的高度为m米，则m=，并求y与x函数表达式；
（3）现公园想通过喷泉设立新的游玩项目，准备通过只调节水管露出湖面的高度，使得游船能从抛物线形水柱下方通过，如图2所示，为避免游船被喷泉淋到，要求游船从抛物线形水柱下方中间通过时，顶棚上任意一点到水柱的竖直距离均不小于0.5米，已知游船顶棚宽度为3米，顶棚到湖面的高度为2米，那么公园应将水管露出湖面的高度（喷水头忽略不计）至少调节到多少米才能符合要求？请通过计算说明理由（结果保留一位小数）．发布：2025/5/23 16:30:1组卷：1253引用：4难度：0.5 -
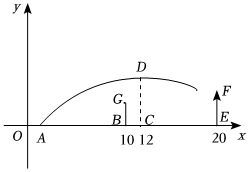2．在某场足球比赛中，球员甲将在地面上点A处的足球对着球门踢出，图中的抛物线是足球的高度y（m）与球和点O的水平距离x（m）的函数y=a（x-h）2+k的部分图象（不考虑空气的阻力），当足球运行到最高点D时，此时球恰好在球员乙的正上方，球员乙在距点O12m的点C处，球距地面的高度为5m,即CD=5m,对方球门与点O的水平距离为20m.
（1）当OA=2时，
①求y与x的关系式；
②当球的高度为3.2m时，求足球与对方球门的水平距离；
（2）防守队员丙站在距点O正前方10m的点B处，球员甲罚出的任意球高过球员丙的头顶并直接射进对方球门，已知丙的身高为1.76m,即BG=1.76m,球门的高度为2.44m,即EF=2.44m,直接写出a的取值范围．发布：2025/5/23 17:0:1组卷：583引用：3难度：0.4 -
3．“城市轨道交通是现代大城市交通的发展方向，发展轨道交通是解决大城市病的有效途径．”如图1，北京地铁（BeijingSubway）是中华人民共和国北京市的城市轨道交通系统，规划于1953年，始建于1965年，运营于1969年，是中国第一个地铁系统．小华了解到列车从慈寿寺站开往花园桥站时，在距离停车线256米处开始减速．他想知道列车从减速开始，经过多少秒停下来，以及最后一秒滑行的距离．为了解决这个问题，小华通过建立函数模型来描述列车离停车线的距离s（米）与滑行时间t（秒）的函数关系，再应用该函数解决相应的问题．
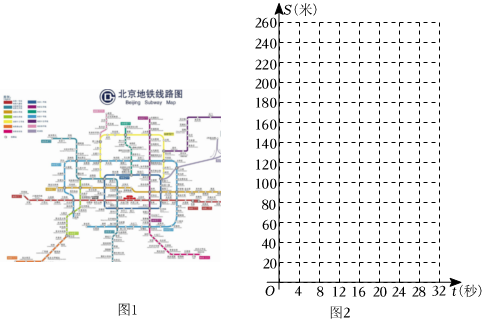
（1）建立模型
①收集数据
②建立平面直角坐标系r（秒） 0 4 8 12 16 20 24 … s（米） 256 196 144 100 64 36 16 …
为了观察s（米）与t（秒）的关系，建立如图2所示的平面直角坐标系．
③描点连线
请在平面直角坐标系中将表中未描出的点补充完整，并用平滑的曲线依次连接．
④选择函数模型
观察这条曲线的形状，它可能是 函数的图象．
⑤求函数解析式
解：设s=at2+bt+c（a≠0），因为t=0时，s=256，所以c=256，则s=at2+bt+256．
请根据表格中的数据，求a,b的值．
验证：把a,b的值代入s=at2+bt+256中，并将其余几对值代入求出的解析式，发现它们都满足该函数解析式．
（2）应用模型
列车从减速开始经过 秒，列车停止；最后一秒钟，列车滑行的距离为 米．发布：2025/5/23 17:0:1组卷：822引用：5难度：0.4
