已知：如图，AB∥CD，直线EF分别交AB，CD于点G，H，点P为直线EF上的点，连接AP，CP．
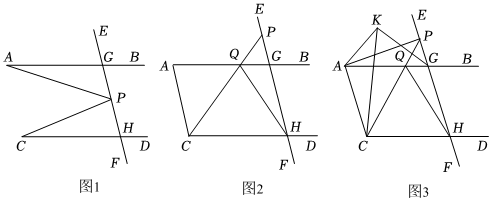
（1）如图1，点P在线段GH上时，请你直接写出∠BAP，∠DCP，∠APC的数量关系；
（2）如图2，点P在HG的延长线上时，连接CP交AB于点Q，连接HQ，AC，若∠ACP+∠PHQ=∠CQH，求证：AC∥EF；
（3）在（2）的条件下，如图3，CK平分∠ACP，GK平分∠AGP，GK与CK交点K，连接AK，若∠PQH=4∠PCK+2∠PHQ，∠CKG=∠CHQ，∠AKC+∠KAC=159°，求∠BAC的大小．
【考点】平行线的判定与性质．
【答案】（1）∠APC=∠BAP+∠DCP；
（2）见详解；
（3）78°．
（2）见详解；
（3）78°．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/24 19:0:2组卷：214引用：3难度：0.5
相似题
-
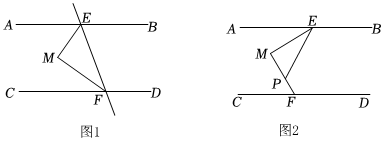1．【发现】如图1，直线AB，CD被直线EF所截，EM平分∠AEF，FM平分∠CFE．若∠AEM=55°，∠CFM=35°，试判断AB与CD平行吗？并说明理由；
【探究】如图2，若直线AB∥CD，点M在直线AB，CD之间，点E，F分别在直线AB，CD上，∠EMF=90°，P是MF上一点，且EM平分∠AEP．若∠CFM=60°，则∠AEP的度数为 ；
【延伸】若直线AB∥CD，点E，F分别在直线AB，CD上，点M在直线AB，CD之间，且在直线EF的左侧，P是折线E-M-F上的一个动点，∠EMF=90°保持不变，移动点P，使EM平分∠AEP或FM平分∠CFP．设∠CFP=α，∠AEP=β，请直接写出α与β之间的数量关系．发布：2025/6/9 8:30:2组卷：511引用：4难度：0.4 -
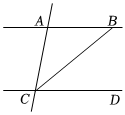2．如图所示，已知∠BAC=100°，CB平分∠ACD．
（1）当添加∠ACD的度数为 时，可判定AB∥CD；
（2）若AB∥CD，则∠ABC的度数为 ．
（3）若AB∥CD，在直线CD上取点E，使∠CAE=∠ACB，则∠AEC的度数为 ．发布：2025/6/9 8:30:2组卷：77引用：2难度：0.5 -
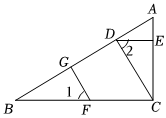3．如图所示，DE⊥AC于点E，BC⊥AC于点C，FG⊥AB于点G，∠1=∠2．
求证：CD⊥AB．
完成下面的证明：
证明：∵DE⊥AC，BC⊥AC（已知）
∴∠AED=∠ACB=90°（ ），
∴DE∥BC（ ），
∴∠2=（ ），
∵∠1=∠2，
∠1=，
∴∥（ ），
∴∠CDB=∠FGB（ ），
∵FG⊥AB（已知），
∴∠FGB=90°=∠CDB，
∴CD⊥AB．发布：2025/6/9 8:30:2组卷：15引用：1难度：0.7
