乘法公式的探究与应用：
（1）如图甲，边长为a的大正方形中有一个边长为b的小正方形，请你写出阴影部分的面积是a2-b2．a2-b2．
（2）小颗将阴影部分接下来，重新拼成一个长方形，如图乙，则长方形的长是a+ba+b，宽是a-ba-b，面积是（a+b）（a-b）（a+b）（a-b）（写成多项式乘法的形式）．
（3）比较甲乙两图阴影部分的面积，可以得到恒等式（a+b）（a-b）=a2-b2．（a+b）（a-b）=a2-b2．
（4）运用你所得到的公式计算：10.3×9.7．
（5）若49x2-y2=25，7x-y=5，则7x+y的值为55
【考点】平方差公式的几何背景；列代数式．
【答案】a2-b2．；a+b；a-b；（a+b）（a-b）；（a+b）（a-b）=a2-b2．；5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：1234引用：2难度：0.4
相似题
-
1．（一）情境再现
借助几何图形探究数量关系，是一种重要的解题策略，图1是用边长分别为a,b的两个正方形和边长为a,b的两个长方形拼成的一个大正方形，利用这一图形可以推导出的乘法公式是 ；（用字母a,b表示）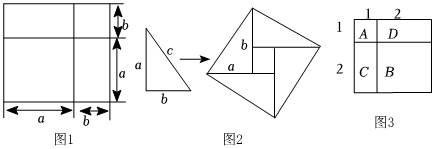
（二）情境延伸
图2是2002年北京世界数学家大会的会标，会标是用边长分别为a,b,c的四个完全相同的直角三角形和一个小正方形拼成的大正方形，利用这一图形可以推导出一个关于a,b,c的怎样结论？并写出简单的推导过程；
（三）问题解决
如图3，A表示的是边长为1的一个正方形，面积为12×1=13，B表示的是一个边长为2的正方形，C，D表示的是边长为1和2的两个长方形，B，C，D的面积和为22+2×1×2=22+22=22×2=23，由于A，B，C，D拼成的是一个边长为3的正方形，所以A，B，C，D的面积和可表示为13+23或（1+2）2，所以13+23=（1+2）2．
类比上述分析过程，在图3的基础上推导：13+23+33=？（画出图形，并写出必要的推导过程）
（四）问题猜想13+23+33+…+m3=（直接写出结论，不用进行推导）发布：2025/6/9 12:0:2组卷：70引用：1难度：0.5 -
2．根据图示，回答下列问题
（1）大正方形的面积S是多少？
（2）梯形Ⅱ，Ⅲ的面积SⅡ，SⅢ，分别是多少？发布：2025/6/9 3:0:1组卷：5引用：1难度：0.6 -
3．从边长为a的正方形中剪掉一个边长为b的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）．
（1）上述操作能验证的等式是 ；（请选择正确的一个）
A．a2-2ab+b2=（a-b）2
B．b2+ab=b（a+b）
C．a2-b2=（a+b）（a-b）
D．a2+ab=a（a+b）
（2）应用你从（1）选出的等式，完成下列各题：
①已知x2-4y2=12，x+2y=4，求x的值．
②计算：．（1-122）（1-132）（1-142）…（1-120202）（1-120212）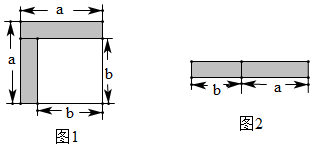
发布：2025/6/9 6:30:1组卷：1323引用：8难度：0.6
