n个有次序的实数a1，a2，…，an所组成的有序数组（a1，a2，…，an）称为一个n维向量，其中ai（i=1，2，…，n）称为该向量的第i个分量．特别地，对一个n维向量a=（a1，a2，…，an），若|ai|=1，i=1，2…n,称a为n维信号向量．设a=（a1，a2，…，an），b=（b1，b2，…，bn），
则a和b的内积定义为a•b=n∑i=1aibi=a1b1+a2b2+…+anbn，且a⊥b⇔a•b=0．
（1）直接写出4个两两垂直的4维信号向量．
（2）证明：不存在14个两两垂直的14维信号向量．
（3）已知k个两两垂直的2024维信号向量x1，x2，…，xk满足它们的前m个分量都是相同的，求证：km＜45．
a
=
（
a
1
，
a
2
，…，
a
n
）
a
a
=
（
a
1
，
a
2
，…，
a
n
）
b
=
（
b
1
，
b
2
，…，
b
n
）
a
b
a
•
b
=
n
∑
i
=
1
a
i
b
i
=
a
1
b
1
+
a
2
b
2
+
…
+
a
n
b
n
a
⊥
b
⇔
a
•
b
km
【考点】平面向量的综合题．
【答案】（1）（1，1，1，1），（-1，-1，1，1），（-1，1，-1，1），（-1，1，1，-1）；
（2）证明见解析；
（3）证明见解析．
（2）证明见解析；
（3）证明见解析．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/20 0:0:1组卷：126引用：11难度：0.3
相似题
-
1．已知
=（1，0），a=（-b，-32），12=（c，-32），x12+ya+zb=（1，1），则x2+y2+z2的最小值．c发布：2024/12/29 13:0:1组卷：193引用：3难度：0.5 -
2．对于空间向量
，定义m=（a,b,c），其中max{x,y,z}表示x,y,z这三个数的最大值．||m||=max{|a|，|b|，|c|}
（Ⅰ）已知，a=（3，-4，2）．b=（x,-x,2x）
①直接写出和||a||（用含x的式子表示）；||b||
②当0≤x≤4，写出的最小值及此时x的值；||a-b||
（Ⅱ）设，a=（x1，y1，z1），求证：b=（x2，y2，z2）；||a+b||≤||a||+||b||
（Ⅲ）在空间直角坐标系O-xyz中，A（2，0，0），B（0，2，0），C（0，0，2），点Q是△ABC内部的动点，直接写出的最小值（无需解答过程）．||OQ||发布：2024/10/21 12:0:1组卷：94引用：2难度：0.3 -
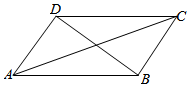3．如图，在平行四边形ABCD中，||=3，|AB|=2，BC=e1，AB|AB|=e2，AD|AD|与AB的夹角为AD．π3
（1）若=xAC+ye1，求x、y的值；e2
（2）求•AC的值；BD
（3）求与AC的夹角的余弦值．BD发布：2024/12/29 1:30:1组卷：983引用：10难度：0.1
