已知a1，a2是平面内任意两个非零不共线向量，过平面内任一点O作OA1=a1，OA2=a2，以O为原点，分别以射线OA1、OA2为x、y轴的正半轴，建立平面坐标系，如图（1）．我们把这个由基底a1，a2确定的坐标系xOy称为基底{a1，a2}坐标系xOy.当向量a1，a2不垂直时，坐标系xOy就是平面斜坐标系，简记为{O；a1，a2}．对平面内任一点P，连结OP，由平面向量基本定理可知，存在唯一实数对（x,y），使得OP=xa1+ya2，则称实数对（x,y）为点P在斜坐标系{O；a1，a2}中的坐标．
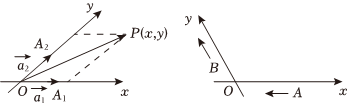
今有斜坐标系{O；e1，e2}（长度单位为米，如图（2）），且|e1|=|e2|=1，〈e1，e2〉=120°，设Op=（1，2）
（1）计算|OP|的大小；
（2）质点甲在ox上距O点4米的点A处，质点乙在oy上距O点1米的点B处，现在甲沿xo的方向，乙沿oy的方向同时以3米/小时的速度移动．
①若过2小时后质点甲到达C点，质点乙到达D点，请用e1，e2，表示CD；
②若t时刻，质点甲到达M点，质点乙到达N点，求两质点何时相距最短，并求出最短距离．
a
1
a
2
O
A
1
=
a
1
O
A
2
=
a
2
a
1
a
2
{
a
1
，
a
2
}
a
1
a
2
{
O
；
a
1
，
a
2
}
OP
=
x
a
1
+
y
a
2
{
O
；
a
1
，
a
2
}
{
O
；
e
1
，
e
2
}
|
e
1
|
=
|
e
2
|
=
1
〈
e
1
，
e
2
〉
=
120
°
O
p
=
（
1
，
2
）
|
OP
|
xo
oy
e
1
e
2
CD
【考点】用平面向量的基底表示平面向量．
【答案】（1）；
（2）①=2+7．；②，．
3
（2）①
CD
e
1
e
2
1
2
5
3
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/13 8:0:8组卷：165引用：10难度：0.7
相似题
-
1．如图，在△OAB中，G为中线OM上一点，且，过点G的直线与边OA，OB分别交于点P，Q．OG=2GM
（Ⅰ）用向量，OA表示OB；OG
（Ⅱ）设向量，OA=43OP，求n的值．OB=nOQ发布：2024/12/29 8:30:1组卷：678引用：6难度：0.7 -
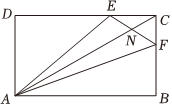2．如图矩形ABCD，，DE=2EC，AC与EF交于点N．BF=2FC
（1）若，求λ+μ的值；CN=λAB+μAD
（2）设，AE=a，试用AF=b，a表示b．AC发布：2024/12/29 4:30:2组卷：20引用：2难度：0.6 -
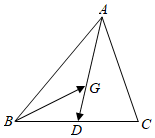3．如图，在△ABC中，点D是边BC的中点，，则用向量AG=2GD表示AB，AC为（ ）BG发布：2024/12/29 8:30:1组卷：728引用：13难度：0.8
