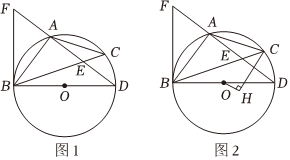
已知：BD为⊙O的直径，O为圆心，点A为圆上一点，过点B作⊙O的切线交DA的延长线于点F，点C为⊙O上一点，且AB=AC，连接BC交AD于点E，连接AC．
（1）如图1，求证：∠ABF=∠ABC．
（2）如图2，点H为⊙O内部一点，连接OH，CH，若∠OHC=90°，CH=12DA时，求∠HCA．
（3）在（2）的条件下，若OH=6，⊙O的半径为10，求CE的长．
1
2
【考点】圆的综合题．
【答案】（1）证明见解答过程；
（2）∠HCA=90°；
（3）．
（2）∠HCA=90°；
（3）
21
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/1 8:0:9组卷：51引用：1难度：0.5
相似题
-
1．在平面直角坐标系xOy中，对于点C和圆P，给出如下定义：
若圆P上存在A、B两点，使得△ABC是等腰直角三角形，且∠ABC=90°，则称点C是圆P的“等垂点”．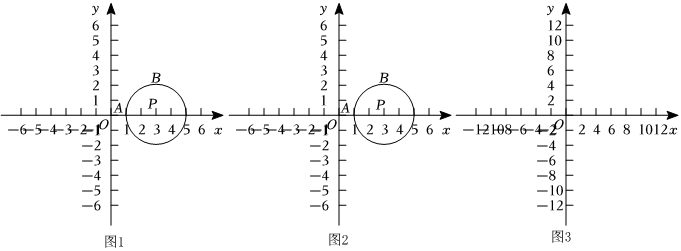
（1）当点P坐标为（3，0），且圆P的半径为2时．
①如图1，若圆P上存在两点A（1，0）和B（3，2），请直接写出此时圆P的“等垂点”C的坐标 ；
②如图2，若直线y=x+b上存在圆P的“等垂点”，求b的取值范围；
（2）设圆P的圆心P在y轴上，半径为2．
若直线y=-x上存在点R，使半径为1的圆R上有点S是圆P的“等垂点”，请直接写出圆心P的纵坐标的取值范围．发布：2025/6/9 12:30:2组卷：127引用：3难度：0.4 -
2．综合与实践
问题情境：如图，将一个圆锥的侧面展开后可得到一个圆心角为n°，半径为l的扇形BOB′，圆锥底面是一个半径为r的圆．母线OA在展开图上对应的半径OA′经过的中点．ˆBB′
特例研究：（1）当r=3，l=9时，n= ，展开图上，OA′与OB的夹角为 °．
问题提出：（2）求证：n=．360rl
问题解决：（3）如图2，一种纸质圆锥形生日帽，底面直径为12cm,母线长也为12cm,为了美观，想在底面圆上一点A和与之相对的母线PB中点C之间拉一条细彩带进行装饰，求彩带长度的最小值．（提示：尝试画出圆锥侧面展开图）发布：2025/6/9 7:30:1组卷：130引用：2难度：0.4 -
3．定义：对角线互相垂直的圆内接四边形称为圆的神奇四边形．
（1）如图1，已知四边形ABCD是⊙O的神奇四边形，若AC=12，BD=10，则S四边形ABCD=；
（2）如图2，已知四边形ABCD为⊙O的内接四边形，连接OA，OB，OC，OD，满足∠BOC+∠AOD=180°，求证：四边形ABCD是⊙O的神奇四边形；
（3）如图3，已知四边形ABCD是⊙O的神奇四边形，∠BAD=90°，延长AD，BC相交于点E，若AB=6，AE=8，求AC的长．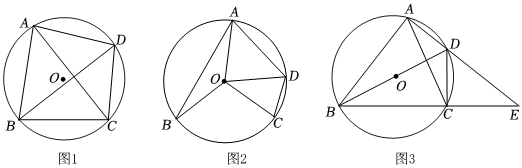
发布：2025/6/9 7:0:1组卷：213引用：1难度：0.6
