当前位置:
知识点挑题
请展开查看知识点列表
>
<
更多>>
|
原创
 更新中
更新中
|
明确考点
剖析考向
配加典例和变式题
真题演练及精选模拟
全方位助力备考
浏览次数:2289
更新:2025年06月13日
|
|
原创
 更新中
更新中
|
知识图解
新知探究
答疑解惑
针对训练
浏览次数:73
更新:2025年06月13日
|
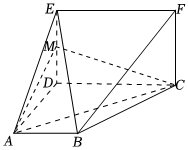 161.如图,平面ABCD⊥平面CDEF,且四边形ABCD是梯形,四边形CDEF是矩形,∠BAD=∠CDA=90°,AB=AD=,M是线段DE上的点,满足DM=2ME.DE=12CD
161.如图,平面ABCD⊥平面CDEF,且四边形ABCD是梯形,四边形CDEF是矩形,∠BAD=∠CDA=90°,AB=AD=,M是线段DE上的点,满足DM=2ME.DE=12CD
(1)证明:BE∥平面MAC;
(2)求直线BF与平面MAC所成角的正弦值.发布:2025/1/2 8:0:1组卷:129引用:1难度:0.4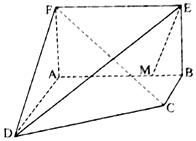 162.如图,在空间几何体ABCDFE中,四边形ABCD为直角梯形,四边形ABEF为矩形,AB=AD=2,AF=BC=1,BC∥AD,AB⊥AD,BC⊥BE,=3AM.MB
162.如图,在空间几何体ABCDFE中,四边形ABCD为直角梯形,四边形ABEF为矩形,AB=AD=2,AF=BC=1,BC∥AD,AB⊥AD,BC⊥BE,=3AM.MB
(1)证明:CF⊥ME;
(2)求三棱锥C-DEF的体积.发布:2025/1/2 8:0:1组卷:72引用:1难度:0.6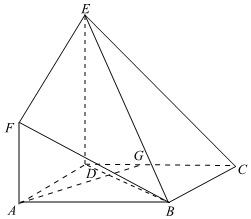 163.如图,在多面体ABCDEF中,四边形ADEF是梯形,四边形ABCD为矩形,DE⊥面ABCD,AF∥DE,AF=AD=DE=1,AB=12.2
163.如图,在多面体ABCDEF中,四边形ADEF是梯形,四边形ABCD为矩形,DE⊥面ABCD,AF∥DE,AF=AD=DE=1,AB=12.2
(1)求证:BF∥平面CDE;
(2)点G为线段CD的中点,求证:AG⊥面DBE.发布:2025/1/2 8:0:1组卷:348引用:1难度:0.6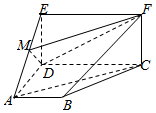 164.如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=CD=2,M是线段AE上的动点.12
164.如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=CD=2,M是线段AE上的动点.12
(Ⅰ)试确定点M的位置,使AC∥平面MDF,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求平面MDF将几何体ADE-BCF分成的两部分的体积之比.发布:2025/1/2 8:0:1组卷:1935引用:12难度:0.1165.下列语句是命题的是( )
发布:2025/1/2 8:0:1组卷:33引用:4难度:0.9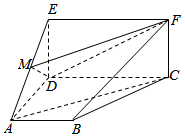 166.如图,四边形ABCD为梯形,四边形CDEF为矩形,平面ABCD⊥平面CDEF,∠BAD=∠ADC=90°,AB=AD=DE=CD,M为AE的中点.12
166.如图,四边形ABCD为梯形,四边形CDEF为矩形,平面ABCD⊥平面CDEF,∠BAD=∠ADC=90°,AB=AD=DE=CD,M为AE的中点.12
(1)证明:AC∥平面MDF;
(2)求平面MDF与平面BCF的夹角的大小.发布:2025/1/2 8:0:1组卷:141引用:1难度:0.6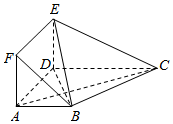 167.在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,CD⊥AD,面ABCD⊥面ADEF,AB=AD=1.CD=2.
167.在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,CD⊥AD,面ABCD⊥面ADEF,AB=AD=1.CD=2.
(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;若不存在,说明理由?3EM=EC
(3)在(2)的条件下,求点A到平面MBC的距离.发布:2025/1/2 8:0:1组卷:109引用:1难度:0.3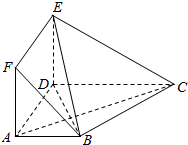 168.在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形.AB∥DC,AB=AD=1,CD=2,AC=EC=.5
168.在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形.AB∥DC,AB=AD=1,CD=2,AC=EC=.5
(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;不存在,请说明理由.发布:2025/1/2 8:0:1组卷:121引用:1难度:0.3169.设命题p:梯形的对角线相等,则¬p为( )
发布:2025/1/2 8:0:1组卷:39引用:1难度:0.9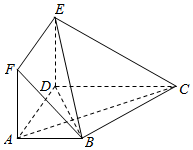 170.在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=.5
170.在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=.5
(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,3=EM,求二面角M-BD-E的平面角的余弦值.EC发布:2025/1/2 8:0:1组卷:562引用:6难度:0.3



