高中数学知识点总结_高中数学知识点试题

当前位置：知识点挑题

请展开查看知识点列表

预备知识
函数
几何与代数
概率与统计
数学知识的延伸

更多>>

原创

更新中

【优学堂】2026年高考数学一轮复习

明确考点剖析考向配加典例和变式题真题演练及精选模拟全方位助力备考

浏览次数：3792 更新：2025年06月20日

原创

更新中

《黄金讲练》2025-2026学年人教A版（2019）必修第一册高一同步课堂

知识图解新知探究答疑解惑针对训练

浏览次数：582 更新：2025年06月20日

2111．已知函数f（x）=2sin（ωx+φ）-1（ω＞0，|φ|＜π）的一个零点是
x
=
π
3
，其图象上一条对称轴方程为
x
=
-
π
6
，则当ω取最小值时，下列说法正确的是（　　）

A．当

∈

[

，-

]

时，函数f（x）单调递增

B．当

∈

[

，

]

时，函数f（x）单调递减

C．函数f（x）的图象关于点

（

，-

）

对称

D．函数f（x）的图象关于直线

对称

发布：2024/12/29 0:30:2组卷：145引用：3难度：0.5

解析

2112．设m,n为两条不同的直线，α，β为两个不同的平面，则下列结论正确的是（　　）
A．α⊥β，m⊥α，n⊥β，则m⊥n B．α⊥β，m⊥α，n⊂β，则m⊥n
C．α⊥β，m⊂α，n⊂β，则m⊥n D．α∥β，m⊂α，n⊂β，则m∥n
发布：2024/12/29 0:30:2组卷：296引用：5难度：0.6
解析
2113．已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示．
（1）求函数y=f（x）的解析式；
（2）求函数y=f（x）的单调增区间；
（3）求方程f（x）=0的解集．
发布：2024/12/29 0:30:2组卷：202引用：5难度：0.5
解析
2114．已知函数f（x）=sin（2x+φ）（-π＜φ＜0），将函数f（x）图象向左平移
π
3
个单位长度后所得的函数图象过点P（0，1），则函数f（x）=sin（2x+φ）（　　）
A．在区间[
π
6
，
π
3
]上单调递减
B．在区间[
π
6
，
π
3
]上单调递增
C．在区间[
-
π
3
，
π
6
]上单调递减
D．在区间[-
5
π
6
，-
2
π
3
]上单调递增
发布：2024/12/29 0:30:2组卷：155引用：5难度：0.8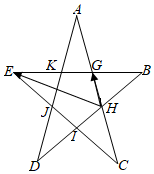
解析
2115．已知由sin2x=2sinxcosx,cos2x=2cos²x-1，cos3x=cos（2x+x）推得三倍角余弦公式cos3x=4cos³x-3cosx,已知cos54°=sin36°，结合三倍角余弦公式和二倍角正弦公式得sin18°=
，如图，已知五角形ABCDE是由边长为2的正五边形GHIJK和五个全等的等腰三角形组成的，则
HG
•
HE
=
．
发布：2024/12/29 0:30:2组卷：205引用：4难度：0.4
解析
2116．已知点P（sin
3
π
4
，cos
3
π
4
）落在角θ的终边上，且θ∈[0，2π]，则θ的值为（　　）
A．
π
4
B．
3
π
4
C．
5
π
4
D．
7
π
4
发布：2024/12/29 0:30:2组卷：247引用：6难度：0.9
解析
2117．已知tanα=-
3
，
π
2
＜α＜π，那么cosα-sinα的值是（　　）
A．-
1
+
3
2
B．
-
1
+
3
2
C．
1
-
3
2
D．
1
+
3
2
发布：2024/12/29 0:30:2组卷：118引用：13难度：0.7
解析
2118．设函数
f
（
x
）
=
2
sin
（
ωx
-
π
3
）
（
ω
＞
0
）
，若对任意的实数x,
f
（
x
）
≤
f
（
π
6
）
恒成立，则ω取最小值时，f（π）=（　　）
A．
2
B．
3
C．-
2
D．-
3
发布：2024/12/29 0:30:2组卷：163引用：7难度：0.7
解析

2119．某科研课题组通过一款手机APP软件，调查了某市1000名跑步爱好者平均每周的跑步量（简称“周跑量”），得到如下的频数分布表：

周跑量
（km/周） [10，15） [15，20） [20，25） [25，30） [30，35） [35，40） [40，45） [45，50） [50，55）

人数 100 120 130 180 220 150 60 30 10

（1）补全该市1000名跑步爱好者周跑量的频率分布直方图；
（2）根据以上图表数据，试求样本的中位数（保留一位小数）；
（3）根据跑步爱好者的周跑量，将跑步爱好者分成以下三类，不同类别的跑者购买的装备的价格不一样，如表：

周跑量小于20公里 20公里到40公里不小于40公里

类别休闲跑者核心跑者精英跑者

装备价格（单位：元） 2500 4000 4500

根据以上数据，估计该市每位跑步爱好者购买装备，平均需要花费多少元？

发布：2024/12/29 0:30:2组卷：115引用：9难度：0.7

解析

2120．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示
（1）求函数f（x）的解析式；
（2）求方程
f
（
x
）
=
-
1
2
在区间[0，4]内的所有实数根之和．
发布：2024/12/29 0:30:2组卷：103引用：3难度：0.6
解析

首页上一页 …209 210 211 212 …下一页尾页

A．α⊥β，m⊥α，n⊥β，则m⊥n	B．α⊥β，m⊥α，n⊂β，则m⊥n
C．α⊥β，m⊂α，n⊂β，则m⊥n	D．α∥β，m⊂α，n⊂β，则m∥n

周跑量（km/周）	[10，15）	[15，20）	[20，25）	[25，30）	[30，35）	[35，40）	[40，45）	[45，50）	[50，55）
人数	100	120	130	180	220	150	60	30	10

周跑量	小于20公里	20公里到40公里	不小于40公里
类别	休闲跑者	核心跑者	精英跑者
装备价格（单位：元）	2500	4000	4500

2111．已知函数f（x）=2sin（ωx+φ）-1（ω＞0，|φ|＜π）的一个零点是x=π3，其图象上一条对称轴方程为x=-π6，则当ω取最小值时，下列说法正确的是（ ）

2112．设m,n为两条不同的直线，α，β为两个不同的平面，则下列结论正确的是（ ）

2113．已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜π2）的部分图象如图所示．（1）求函数y=f（x）的解析式；（2）求函数y=f（x）的单调增区间；（3）求方程f（x）=0的解集．

2114．已知函数f（x）=sin（2x+φ）（-π＜φ＜0），将函数f（x）图象向左平移π3个单位长度后所得的函数图象过点P（0，1），则函数f（x）=sin（2x+φ）（ ）

2116．已知点P（sin3π4，cos3π4）落在角θ的终边上，且θ∈[0，2π]，则θ的值为（ ）

2117．已知tanα=-3，π2＜α＜π，那么cosα-sinα的值是（ ）

2118．设函数f（x）=2sin（ωx-π3）（ω＞0），若对任意的实数x,f（x）≤f（π6）恒成立，则ω取最小值时，f（π）=（ ）

2120．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π2）的部分图象如图所示（1）求函数f（x）的解析式；（2）求方程f（x）=-12在区间[0，4]内的所有实数根之和．

2111．已知函数f（x）=2sin（ωx+φ）-1（ω＞0，|φ|＜π）的一个零点是
x
=
π
3
，其图象上一条对称轴方程为
x
=
-
π
6
，则当ω取最小值时，下列说法正确的是（　　）

2112．设m,n为两条不同的直线，α，β为两个不同的平面，则下列结论正确的是（　　）

2113．已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示．
（1）求函数y=f（x）的解析式；
（2）求函数y=f（x）的单调增区间；
（3）求方程f（x）=0的解集．

2114．已知函数f（x）=sin（2x+φ）（-π＜φ＜0），将函数f（x）图象向左平移
π
3
个单位长度后所得的函数图象过点P（0，1），则函数f（x）=sin（2x+φ）（　　）

2116．已知点P（sin
3
π
4
，cos
3
π
4
）落在角θ的终边上，且θ∈[0，2π]，则θ的值为（　　）

2117．已知tanα=-
3
，
π
2
＜α＜π，那么cosα-sinα的值是（　　）

2118．设函数
f
（
x
）
=
2
sin
（
ωx
-
π
3
）
（
ω
＞
0
）
，若对任意的实数x,
f
（
x
）
≤
f
（
π
6
）
恒成立，则ω取最小值时，f（π）=（　　）

2120．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示
（1）求函数f（x）的解析式；
（2）求方程
f
（
x
）
=
-
1
2
在区间[0，4]内的所有实数根之和．